10.9. The SUNMATRIX_DENSE Module

The dense implementation of the SUNMatrix module, SUNMATRIX_DENSE, defines the content field of SUNMatrix to be the following structure:

struct _SUNMatrixContent_Dense {
  sunindextype M;
  sunindextype N;
  sunrealtype *data;
  sunindextype ldata;
  sunrealtype **cols;
};

These entries of the content field contain the following information:

M - number of rows
N - number of columns
data - pointer to a contiguous block of sunrealtype variables. The elements of the dense matrix are stored columnwise, i.e. the \((i,j)\) element of a dense SUNMatrix object (with \(0 \le i < M\) and \(0 \le j < N\)) may be accessed via data[j*M+i].
ldata - length of the data array (\(= M\, N\)).
cols - array of pointers. cols[j] points to the first element of the j-th column of the matrix in the array data. The \((i,j)\) element of a dense SUNMatrix (with \(0 \le i < M\) and \(0 \le j < N\)) may be accessed may be accessed via cols[j][i].

The header file to be included when using this module is sunmatrix/sunmatrix_dense.h.

The following macros are provided to access the content of a SUNMATRIX_DENSE matrix. The prefix SM_ in the names denotes that these macros are for SUNMatrix implementations, and the suffix _D denotes that these are specific to the dense version.

SM_CONTENT_D(A)

This macro gives access to the contents of the dense SUNMatrix A.

The assignment A_cont = SM_CONTENT_D(A) sets A_cont to be a pointer to the dense SUNMatrix content structure.

Implementation:

#define SM_CONTENT_D(A)   ( (SUNMatrixContent_Dense)(A->content) )

SM_ROWS_D(A)

Access the number of rows in the dense SUNMatrix A.

This may be used either to retrieve or to set the value. For example, the assignment A_rows = SM_ROWS_D(A) sets A_rows to be the number of rows in the matrix A. Similarly, the assignment SM_ROWS_D(A) = A_rows sets the number of columns in A to equal A_rows.

Implementation:

#define SM_ROWS_D(A)   ( SM_CONTENT_D(A)->M )

SM_COLUMNS_D(A)

Access the number of columns in the dense SUNMatrix A.

This may be used either to retrieve or to set the value. For example, the assignment A_columns = SM_COLUMNS_D(A) sets A_columns to be the number of columns in the matrix A. Similarly, the assignment SM_COLUMNS_D(A) = A_columns sets the number of columns in A to equal A_columns

Implementation:

#define SM_COLUMNS_D(A)   ( SM_CONTENT_D(A)->N )

SM_LDATA_D(A)

Access the total data length in the dense SUNMatrix A.

This may be used either to retrieve or to set the value. For example, the assignment A_ldata = SM_LDATA_D(A) sets A_ldata to be the length of the data array in the matrix A. Similarly, the assignment SM_LDATA_D(A) = A_ldata sets the parameter for the length of the data array in A to equal A_ldata.

Implementation:

#define SM_LDATA_D(A)   ( SM_CONTENT_D(A)->ldata )

SM_DATA_D(A)

This macro gives access to the data pointer for the matrix entries.

The assignment A_data = SM_DATA_D(A) sets A_data to be a pointer to the first component of the data array for the dense SUNMatrix A. The assignment SM_DATA_D(A) = A_data sets the data array of A to be A_data by storing the pointer A_data.

Implementation:

#define SM_DATA_D(A)   ( SM_CONTENT_D(A)->data )

SM_COLS_D(A)

This macro gives access to the cols pointer for the matrix entries.

The assignment A_cols = SM_COLS_D(A) sets A_cols to be a pointer to the array of column pointers for the dense SUNMatrix A. The assignment SM_COLS_D(A) = A_cols sets the column pointer array of A to be A_cols by storing the pointer A_cols.

Implementation:

#define SM_COLS_D(A)   ( SM_CONTENT_D(A)->cols )

SM_COLUMN_D(A)

This macros gives access to the individual columns of the data array of a dense SUNMatrix.

The assignment col_j = SM_COLUMN_D(A,j) sets col_j to be a pointer to the first entry of the j-th column of the \(M \times N\) dense matrix A (with \(0 \le j < N\)). The type of the expression SM_COLUMN_D(A,j) is sunrealtype *. The pointer returned by the call SM_COLUMN_D(A,j) can be treated as an array which is indexed from 0 to M-1.

Implementation:

#define SM_COLUMN_D(A,j)    ( (SM_CONTENT_D(A)->cols)[j] )

SM_ELEMENT_D(A)

This macro gives access to the individual entries of the data array of a dense SUNMatrix.

The assignments SM_ELEMENT_D(A,i,j) = a_ij and a_ij = SM_ELEMENT_D(A,i,j) reference the \(A_{i,j}\) element of the \(M \times N\) dense matrix A (with \(0 \le i < M\) and \(0 \le j < N\)).

Implementation:

#define SM_ELEMENT_D(A,i,j) ( (SM_CONTENT_D(A)->cols)[j][i] )

The SUNMATRIX_DENSE module defines dense implementations of all matrix operations listed in §10.2. Their names are obtained from those in that section by appending the suffix _Dense (e.g. SUNMatCopy_Dense). The module SUNMATRIX_DENSE provides the following additional user-callable routines:

SUNMatrix SUNDenseMatrix(sunindextype M, sunindextype N, SUNContext sunctx): This constructor function creates and allocates memory for a dense SUNMatrix. Its arguments are the number of rows, M, and columns, N, for the dense matrix.

void SUNDenseMatrix_Print(SUNMatrix A, FILE *outfile): This function prints the content of a dense SUNMatrix to the output stream specified by outfile. Note: stdout or stderr may be used as arguments for outfile to print directly to standard output or standard error, respectively.

sunindextype SUNDenseMatrix_Rows(SUNMatrix A): This function returns the number of rows in the dense SUNMatrix.

sunindextype SUNDenseMatrix_Columns(SUNMatrix A): This function returns the number of columns in the dense SUNMatrix.

sunindextype SUNDenseMatrix_LData(SUNMatrix A): This function returns the length of the data array for the dense SUNMatrix.

sunrealtype *SUNDenseMatrix_Data(SUNMatrix A): This function returns a pointer to the data array for the dense SUNMatrix.

sunrealtype **SUNDenseMatrix_Cols(SUNMatrix A): This function returns a pointer to the cols array for the dense SUNMatrix.

sunrealtype *SUNDenseMatrix_Column(SUNMatrix A, sunindextype j): This function returns a pointer to the first entry of the jth column of the dense SUNMatrix. The resulting pointer should be indexed over the range 0 to M-1.

Notes

When looping over the components of a dense SUNMatrix A, the most efficient approaches are to:
- First obtain the component array via A_data = SUNDenseMatrix_Data(A), or equivalently A_data = SM_DATA_D(A), and then access A_data[i] within the loop.
- First obtain the array of column pointers via A_cols = SUNDenseMatrix_Cols(A), or equivalently A_cols = SM_COLS_D(A), and then access A_cols[j][i] within the loop.
- Within a loop over the columns, access the column pointer via A_colj = SUNDenseMatrix_Column(A,j) and then to access the entries within that column using A_colj[i] within the loop.
All three of these are more efficient than using SM_ELEMENT_D(A,i,j) within a double loop.
Within the SUNMatMatvec_Dense routine, internal consistency checks are performed to ensure that the matrix is called with consistent N_Vector implementations. These are currently limited to: NVECTOR_SERIAL, NVECTOR_OPENMP, and NVECTOR_PTHREADS. As additional compatible vector implementations are added to SUNDIALS, these will be included within this compatibility check.

10.10. The SUNMATRIX_MAGMADENSE Module

The SUNMATRIX_MAGMADENSE module interfaces to the MAGMA linear algebra library and can target NVIDIA’s CUDA programming model or AMD’s HIP programming model [122]. All data stored by this matrix implementation resides on the GPU at all times. The implementation currently supports a standard LAPACK column-major storage format as well as a low-storage format for block-diagonal matrices

\[\begin{split}\mathbf{A} = \begin{bmatrix} \mathbf{A_0} & 0 & \cdots & 0\\ 0 & \mathbf{A_2} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \mathbf{A_{n-1}}\\ \end{bmatrix}\end{split}\]

This matrix implementation is best paired with the SUNLinearSolver_MagmaDense SUNLinearSolver.

The header file to include when using this module is sunmatrix/sunmatrix_magmadense.h. The installed library to link to is libsundials_sunmatrixmagmadense.lib where lib is typically .so for shared libraries and .a for static libraries.

Warning

The SUNMATRIX_MAGMADENSE module is experimental and subject to change.

10.10.1. SUNMATRIX_MAGMADENSE Functions

The SUNMATRIX_MAGMADENSE module defines GPU-enabled implementations of all matrix operations listed in §10.2.

SUNMatGetID_MagmaDense – returns SUNMATRIX_MAGMADENSE
SUNMatClone_MagmaDense
SUNMatDestroy_MagmaDense
SUNMatZero_MagmaDense
SUNMatCopy_MagmaDense
SUNMatScaleAdd_MagmaDense
SUNMatScaleAddI_MagmaDense
SUNMatMatvecSetup_MagmaDense
SUNMatMatvec_MagmaDense
SUNMatSpace_MagmaDense

In addition, the SUNMATRIX_MAGMADENSE module defines the following implementation specific functions:

SUNMatrix SUNMatrix_MagmaDense(sunindextype M, sunindextype N, SUNMemoryType memtype, SUNMemoryHelper memhelper, void *queue, SUNContext sunctx)

This constructor function creates and allocates memory for an \(M \times N\) SUNMATRIX_MAGMADENSE SUNMatrix.

Arguments:

M – the number of matrix rows.
N – the number of matrix columns.
memtype – the type of memory to use for the matrix data; can be SUNMEMTYPE_UVM or SUNMEMTYPE_DEVICE.
memhelper – the memory helper used for allocating data.
queue – a cudaStream_t when using CUDA or a hipStream_t when using HIP.
sunctx – the SUNContext object (see §2.4)

Return value:

If successful, a SUNMatrix object otherwise NULL.

SUNMatrix SUNMatrix_MagmaDenseBlock(sunindextype nblocks, sunindextype M_block, sunindextype N_block, SUNMemoryType memtype, SUNMemoryHelper memhelper, void *queue, SUNContext sunctx)

This constructor function creates and allocates memory for a block diagonal SUNMATRIX_MAGMADENSE SUNMatrix with nblocks of size \(M \times N\).

Arguments:

nblocks – the number of matrix rows.
M_block – the number of matrix rows in each block.
N_block – the number of matrix columns in each block.
memtype – the type of memory to use for the matrix data; can be SUNMEMTYPE_UVM or SUNMEMTYPE_DEVICE.
memhelper – the memory helper used for allocating data.
queue – a cudaStream_t when using CUDA or a hipStream_t when using HIP.
sunctx – the SUNContext object (see §2.4)

Return value:

If successful, a SUNMatrix object otherwise NULL.

sunindextype SUNMatrix_MagmaDense_Rows(SUNMatrix A)

This function returns the number of rows in the SUNMatrix object. For block diagonal matrices, the number of rows is computed as \(M_{\text{block}} \times \text{nblocks}\).

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of rows in the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_MagmaDense_Columns(SUNMatrix A)

This function returns the number of columns in the SUNMatrix object. For block diagonal matrices, the number of columns is computed as \(N_{\text{block}} \times \text{nblocks}\).

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of columns in the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_MagmaDense_BlockRows(SUNMatrix A)

This function returns the number of rows in a block of the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of rows in a block of the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_MagmaDense_BlockColumns(SUNMatrix A)

This function returns the number of columns in a block of the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of columns in a block of the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_MagmaDense_LData(SUNMatrix A)

This function returns the length of the SUNMatrix data array.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the length of the SUNMatrix data array otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_MagmaDense_NumBlocks(SUNMatrix A)

This function returns the number of blocks in the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of blocks in the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunrealtype *SUNMatrix_MagmaDense_Data(SUNMatrix A)

This function returns the SUNMatrix data array.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the SUNMatrix data array otherwise NULL.

sunrealtype **SUNMatrix_MagmaDense_BlockData(SUNMatrix A)

This function returns an array of pointers that point to the start of the data array for each block in the SUNMatrix.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, an array of data pointers to each of the SUNMatrix blocks otherwise NULL.

sunrealtype *SUNMatrix_MagmaDense_Block(SUNMatrix A, sunindextype k)

This function returns a pointer to the data array for block k in the SUNMatrix.

Arguments:

A – a SUNMatrix object.
k – the block index.

Return value:

If successful, a pointer to the data array for the SUNMatrix block otherwise NULL.

Note

No bounds-checking is performed by this function, j should be strictly less than nblocks.

sunrealtype *SUNMatrix_MagmaDense_Column(SUNMatrix A, sunindextype j)

This function returns a pointer to the data array for column j in the SUNMatrix.

Arguments:

A – a SUNMatrix object.
j – the column index.

Return value:

If successful, a pointer to the data array for the SUNMatrix column otherwise NULL.

Note

No bounds-checking is performed by this function, j should be strictly less than \(nblocks * N_{\text{block}}\).

sunrealtype *SUNMatrix_MagmaDense_BlockColumn(SUNMatrix A, sunindextype k, sunindextype j)

This function returns a pointer to the data array for column j of block k in the SUNMatrix.

Arguments:

A – a SUNMatrix object.
k – the block index.
j – the column index.

Return value:

If successful, a pointer to the data array for the SUNMatrix column otherwise NULL.

Note

No bounds-checking is performed by this function, k should be strictly less than nblocks and j should be strictly less than \(N_{\text{block}}\).

SUNErrCode SUNMatrix_MagmaDense_CopyToDevice(SUNMatrix A, sunrealtype *h_data)

This function copies the matrix data to the GPU device from the provided host array.

Arguments:

A – a SUNMatrix object
h_data – a host array pointer to copy data from.

Return value:

SUN_SUCCESS – if the copy is successful.
SUN_ERR_ARG_INCOMPATIBLE – if the SUNMatrix is not a SUNMATRIX_MAGMADENSE matrix.
SUN_ERR_MEM_FAIL – if the copy fails.

SUNErrCode SUNMatrix_MagmaDense_CopyFromDevice(SUNMatrix A, sunrealtype *h_data)

This function copies the matrix data from the GPU device to the provided host array.

Arguments:

A – a SUNMatrix object
h_data – a host array pointer to copy data to.

Return value:

SUN_SUCCESS – if the copy is successful.
SUN_ERR_ARG_INCOMPATIBLE – if the SUNMatrix is not a SUNMATRIX_MAGMADENSE matrix.
SUN_ERR_MEM_FAIL – if the copy fails.

10.10.2. SUNMATRIX_MAGMADENSE Usage Notes

Warning

When using the SUNMATRIX_MAGMADENSE module with a SUNDIALS package (e.g. CVODE), the stream given to matrix should be the same stream used for the NVECTOR object that is provided to the package, and the NVECTOR object given to the SUNMatvec operation. If different streams are utilized, synchronization issues may occur.

10.11. The SUNMATRIX_ONEMKLDENSE Module

The SUNMATRIX_ONEMKLDENSE module is intended for interfacing with direct linear solvers from the Intel oneAPI Math Kernel Library (oneMKL) using the SYCL (DPC++) programming model. The implementation currently supports a standard LAPACK column-major storage format as well as a low-storage format for block-diagonal matrices,

\[\begin{split}\mathbf{A} = \begin{bmatrix} \mathbf{A_0} & 0 & \cdots & 0 \\ 0 & \mathbf{A_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathbf{A_{n-1}} \end{bmatrix}\end{split}\]

This matrix implementation is best paired with the SUNLinearSolver_OneMklDense linear solver.

The header file to include when using this class is sunmatrix/sunmatrix_onemkldense.h. The installed library to link to is libsundials_sunmatrixonemkldense.lib where lib is typically .so for shared libraries and .a for static libraries.

Warning

The SUNMATRIX_ONEMKLDENSE class is experimental and subject to change.

10.11.1. SUNMATRIX_ONEMKLDENSE Functions

The SUNMATRIX_ONEMKLDENSE class defines implementations of the following matrix operations listed in §10.2.

SUNMatGetID_OneMklDense – returns SUNMATRIX_ONEMKLDENSE
SUNMatClone_OneMklDense
SUNMatDestroy_OneMklDense
SUNMatZero_OneMklDense
SUNMatCopy_OneMklDense
SUNMatScaleAdd_OneMklDense
SUNMatScaleAddI_OneMklDense
SUNMatMatvec_OneMklDense
SUNMatSpace_OneMklDense

In addition, the SUNMATRIX_ONEMKLDENSE class defines the following implementation specific functions.

10.11.1.1. Constructors

SUNMatrix SUNMatrix_OneMklDense(sunindextype M, sunindextype N, SUNMemoryType memtype, SUNMemoryHelper memhelper, sycl::queue *queue, SUNContext sunctx)

This constructor function creates and allocates memory for an \(M \times N\) SUNMATRIX_ONEMKLDENSE SUNMatrix.

Arguments:

M – the number of matrix rows.
N – the number of matrix columns.
memtype – the type of memory to use for the matrix data; can be SUNMEMTYPE_UVM or SUNMEMTYPE_DEVICE.
memhelper – the memory helper used for allocating data.
queue – the SYCL queue to which operations will be submitted.
sunctx – the SUNContext object (see §2.4)

Return value:

If successful, a SUNMatrix object otherwise NULL.

SUNMatrix SUNMatrix_OneMklDenseBlock(sunindextype nblocks, sunindextype M_block, sunindextype N_block, SUNMemoryType memtype, SUNMemoryHelper memhelper, sycl::queue *queue, SUNContext sunctx)

This constructor function creates and allocates memory for a block diagonal SUNMATRIX_ONEMKLDENSE SUNMatrix with nblocks of size \(M_{block} \times N_{block}\).

Arguments:

nblocks – the number of matrix rows.
M_block – the number of matrix rows in each block.
N_block – the number of matrix columns in each block.
memtype – the type of memory to use for the matrix data; can be SUNMEMTYPE_UVM or SUNMEMTYPE_DEVICE.
memhelper – the memory helper used for allocating data.
queue – the SYCL queue to which operations will be submitted.
sunctx – the SUNContext object (see §2.4)

Return value:

If successful, a SUNMatrix object otherwise NULL.

10.11.1.2. Access Matrix Dimensions

sunindextype SUNMatrix_OneMklDense_Rows(SUNMatrix A)

This function returns the number of rows in the SUNMatrix object. For block diagonal matrices, the number of rows is computed as \(M_{\text{block}} \times \text{nblocks}\).

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of rows in the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_OneMklDense_Columns(SUNMatrix A)

This function returns the number of columns in the SUNMatrix object. For block diagonal matrices, the number of columns is computed as \(N_{\text{block}} \times \text{nblocks}\).

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of columns in the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

10.11.1.3. Access Matrix Block Dimensions

sunindextype SUNMatrix_OneMklDense_NumBlocks(SUNMatrix A)

This function returns the number of blocks in the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of blocks in the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_OneMklDense_BlockRows(SUNMatrix A)

This function returns the number of rows in a block of the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of rows in a block of the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

sunindextype SUNMatrix_OneMklDense_BlockColumns(SUNMatrix A)

This function returns the number of columns in a block of the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the number of columns in a block of the SUNMatrix object otherwise SUNMATRIX_ILL_INPUT.

10.11.1.4. Access Matrix Data

sunindextype SUNMatrix_OneMklDense_LData(SUNMatrix A)

This function returns the length of the SUNMatrix data array.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the length of the SUNMatrix data array otherwise SUNMATRIX_ILL_INPUT.

sunrealtype *SUNMatrix_OneMklDense_Data(SUNMatrix A)

This function returns the SUNMatrix data array.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the SUNMatrix data array otherwise NULL.

sunrealtype *SUNMatrix_OneMklDense_Column(SUNMatrix A, sunindextype j)

This function returns a pointer to the data array for column j in the SUNMatrix.

Arguments:

A – a SUNMatrix object.
j – the column index.

Return value:

If successful, a pointer to the data array for the SUNMatrix column otherwise NULL.

Note

No bounds-checking is performed by this function, j should be strictly less than \(nblocks * N_{\text{block}}\).

10.11.1.5. Access Matrix Block Data

sunindextype SUNMatrix_OneMklDense_BlockLData(SUNMatrix A)

This function returns the length of the SUNMatrix data array for each block of the SUNMatrix object.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, the length of the SUNMatrix data array for each block otherwise SUNMATRIX_ILL_INPUT.

sunrealtype **SUNMatrix_OneMklDense_BlockData(SUNMatrix A)

This function returns an array of pointers that point to the start of the data array for each block in the SUNMatrix.

Arguments:

A – a SUNMatrix object.

Return value:

If successful, an array of data pointers to each of the SUNMatrix blocks otherwise NULL.

sunrealtype *SUNMatrix_OneMklDense_Block(SUNMatrix A, sunindextype k)

This function returns a pointer to the data array for block k in the SUNMatrix.

Arguments:

A – a SUNMatrix object.
k – the block index.

Return value:

If successful, a pointer to the data array for the SUNMatrix block otherwise NULL.

Note

No bounds-checking is performed by this function, j should be strictly less than nblocks.

sunrealtype *SUNMatrix_OneMklDense_BlockColumn(SUNMatrix A, sunindextype k, sunindextype j)

This function returns a pointer to the data array for column j of block k in the SUNMatrix.

Arguments:

A – a SUNMatrix object.
k – the block index.
j – the column index.

Return value:

If successful, a pointer to the data array for the SUNMatrix column otherwise NULL.

Note

No bounds-checking is performed by this function, k should be strictly less than nblocks and j should be strictly less than \(N_{\text{block}}\).

10.11.1.6. Copy Data

SUNErrCode SUNMatrix_OneMklDense_CopyToDevice(SUNMatrix A, sunrealtype *h_data)

This function copies the matrix data to the GPU device from the provided host array.

Arguments:

A – a SUNMatrix object
h_data – a host array pointer to copy data from.

Return value:

SUN_SUCCESS – if the copy is successful.
SUN_ERR_ARG_INCOMPATIBLE – if the SUNMatrix is not a SUNMATRIX_ONEMKLDENSE matrix.
SUN_ERR_MEM_FAIL – if the copy fails.

SUNErrCode SUNMatrix_OneMklDense_CopyFromDevice(SUNMatrix A, sunrealtype *h_data)

This function copies the matrix data from the GPU device to the provided host array.

Arguments:

A – a SUNMatrix object
h_data – a host array pointer to copy data to.

Return value:

SUN_SUCCESS – if the copy is successful.
SUN_ERR_ARG_INCOMPATIBLE – if the SUNMatrix is not a SUNMATRIX_ONEMKLDENSE matrix.
SUN_ERR_MEM_FAIL – if the copy fails.

10.11.2. SUNMATRIX_ONEMKLDENSE Usage Notes

Warning

The SUNMATRIX_ONEMKLDENSE class only supports 64-bit indexing, thus SUNDIALS must be built for 64-bit indexing to use this class.

When using the SUNMATRIX_ONEMKLDENSE class with a SUNDIALS package (e.g. CVODE), the queue given to matrix should be the same stream used for the NVECTOR object that is provided to the package, and the NVECTOR object given to the SUNMatMatvec() operation. If different streams are utilized, synchronization issues may occur.

10.12. The SUNMATRIX_BAND Module

The banded implementation of the SUNMatrix module, SUNMATRIX_BAND, defines the content field of SUNMatrix to be the following structure:

struct _SUNMatrixContent_Band {
  sunindextype M;
  sunindextype N;
  sunindextype mu;
  sunindextype ml;
  sunindextype smu;
  sunindextype ldim;
  sunrealtype *data;
  sunindextype ldata;
  sunrealtype **cols;
};

A diagram of the underlying data representation in a banded matrix is shown in Fig. 10.1. A more complete description of the parts of this content field is given below:

M - number of rows
N - number of columns (N = M)
mu - upper half-bandwidth, \(0 \le \text{mu} < N\)
ml - lower half-bandwidth, \(0 \le \text{ml} < N\)
smu - storage upper bandwidth, \(\text{mu} \le \text{smu} < N\). The LU decomposition routines in the associated SUNLINSOL_BAND and SUNLINSOL_LAPACKBAND modules write the LU factors into the existing storage for the band matrix. The upper triangular factor \(U\), however, may have an upper bandwidth as big as min(N-1, mu+ml) because of partial pivoting. The smu field holds the upper half-bandwidth allocated for the band matrix.
ldim - leading dimension (\(\text{ldim} \ge smu + ml + 1\))
data - pointer to a contiguous block of sunrealtype variables. The elements of the banded matrix are stored columnwise (i.e. columns are stored one on top of the other in memory). Only elements within the specified half-bandwidths are stored. data is a pointer to ldata contiguous locations which hold the elements within the banded matrix.
ldata - length of the data array (\(= \text{ldim}\, N\))
cols - array of pointers. cols[j] is a pointer to the uppermost element within the band in the j-th column. This pointer may be treated as an array indexed from smu-mu (to access the uppermost element within the band in the j-th column) to smu+ml (to access the lowest element within the band in the j-th column). Indices from 0 to smu-mu-1 give access to extra storage elements required by the LU decomposition function. Finally, cols[j][i-j+smu] is the (\(i,j\))-th element with \(j-\text{mu} \le i \le j+\text{ml}\).

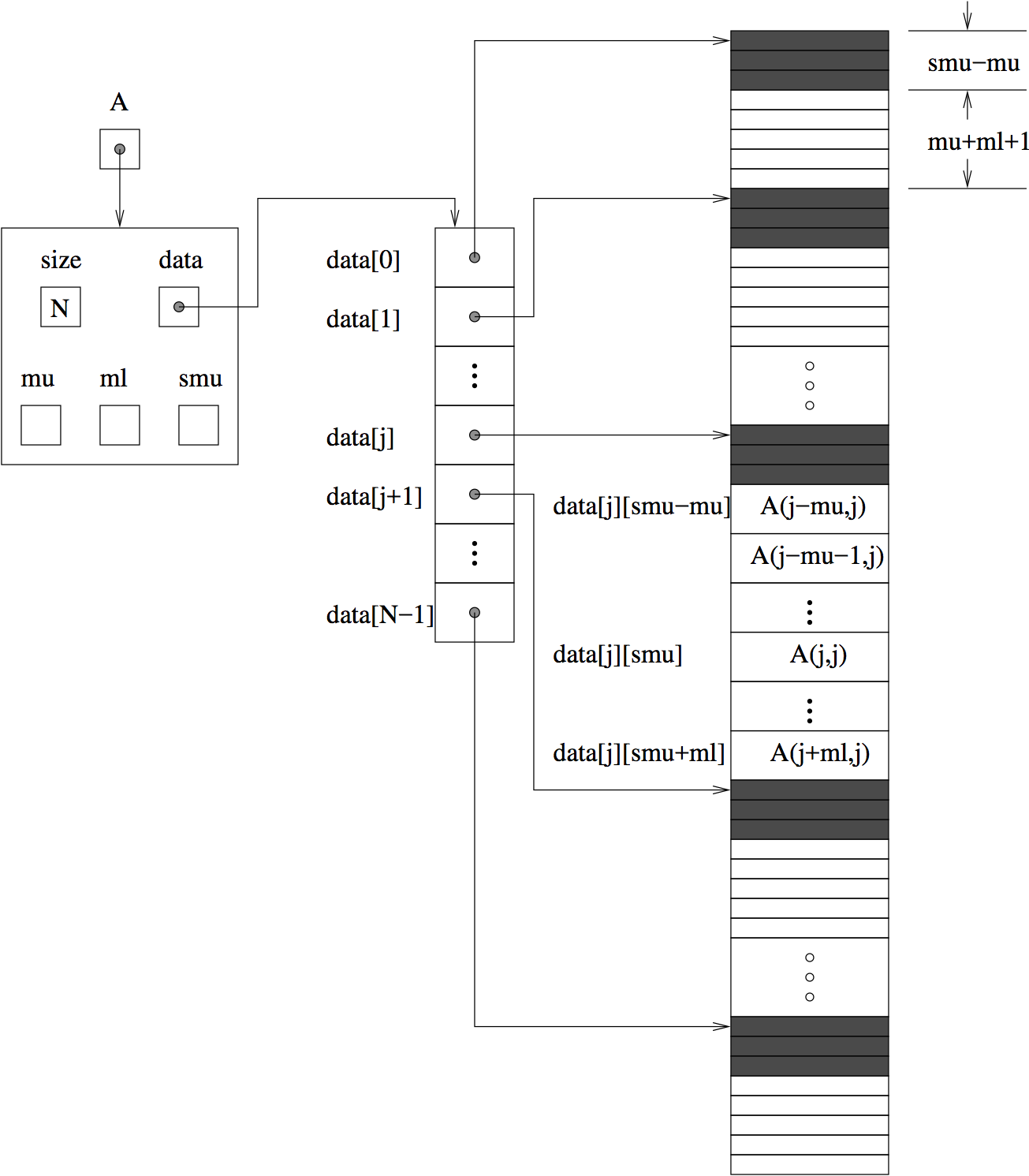
../_images/bandmat.png — Fig. 10.1 Diagram of the storage for the SUNMATRIX_BAND module. Here `A` is an \(N \times N\) band matrix with upper and lower half-bandwidths `mu` and `ml`, respectively. The rows and columns of `A` are numbered from 0 to `N-1` and the (\(i,j\))-th element of `A` is denoted `A(i,j)`. The greyed out areas of the underlying component storage are used by the associated SUNLINSOL_BAND or SUNLINSOL_LAPACKBAND linear solver.

The header file to be included when using this module is sunmatrix/sunmatrix_band.h.

The following macros are provided to access the content of a SUNMATRIX_BAND matrix. The prefix SM_ in the names denotes that these macros are for SUNMatrix implementations, and the suffix _B denotes that these are specific to the banded version.

SM_CONTENT_B(A)

This macro gives access to the contents of the banded SUNMatrix A.

The assignment A_cont = SM_CONTENT_B(A) sets A_cont to be a pointer to the banded SUNMatrix content structure.

Implementation:

#define SM_CONTENT_B(A)   ( (SUNMatrixContent_Band)(A->content) )

SM_ROWS_B(A)

Access the number of rows in the banded SUNMatrix A.

This may be used either to retrieve or to set the value. For example, the assignment A_rows = SM_ROWS_B(A) sets A_rows to be the number of rows in the matrix A. Similarly, the assignment SM_ROWS_B(A) = A_rows sets the number of columns in A to equal A_rows.

Implementation:

#define SM_ROWS_B(A)   ( SM_CONTENT_B(A)->M )

SM_COLUMNS_B(A)

Access the number of columns in the banded SUNMatrix A. As with SM_ROWS_B, this may be used either to retrieve or to set the value.

Implementation:

#define SM_COLUMNS_B(A)   ( SM_CONTENT_B(A)->N )

SM_UBAND_B(A)

Access the mu parameter in the banded SUNMatrix A. As with SM_ROWS_B, this may be used either to retrieve or to set the value.

Implementation:

#define SM_UBAND_B(A)   ( SM_CONTENT_B(A)->mu )

SM_LBAND_B(A)

Access the ml parameter in the banded SUNMatrix A. As with SM_ROWS_B, this may be used either to retrieve or to set the value.

Implementation:

#define SM_LBAND_B(A)   ( SM_CONTENT_B(A)->ml )

SM_SUBAND_B(A)

Access the smu parameter in the banded SUNMatrix A. As with SM_ROWS_B, this may be used either to retrieve or to set the value.

Implementation:

#define SM_SUBAND_B(A)   ( SM_CONTENT_B(A)->smu )

SM_LDIM_B(A)

Access the ldim parameter in the banded SUNMatrix A. As with SM_ROWS_B, this may be used either to retrieve or to set the value.

Implementation:

#define SM_LDIM_B(A)   ( SM_CONTENT_B(A)->ldim )

SM_LDATA_B(A)

Access the ldata parameter in the banded SUNMatrix A. As with SM_ROWS_B, this may be used either to retrieve or to set the value.

Implementation:

#define SM_LDATA_B(A)   ( SM_CONTENT_B(A)->ldata )

SM_DATA_B(A)

This macro gives access to the data pointer for the matrix entries.

The assignment A_data = SM_DATA_B(A) sets A_data to be a pointer to the first component of the data array for the banded SUNMatrix A. The assignment SM_DATA_B(A) = A_data sets the data array of A to be A_data by storing the pointer A_data.

Implementation:

#define SM_DATA_B(A)   ( SM_CONTENT_B(A)->data )

SM_COLS_B(A)

This macro gives access to the cols pointer for the matrix entries.

The assignment A_cols = SM_COLS_B(A) sets A_cols to be a pointer to the array of column pointers for the banded SUNMatrix A. The assignment SM_COLS_B(A) = A_cols sets the column pointer array of A to be A_cols by storing the pointer A_cols.

Implementation:

#define SM_COLS_B(A)   ( SM_CONTENT_B(A)->cols )

SM_COLUMN_B(A)

This macros gives access to the individual columns of the data array of a banded SUNMatrix.

The assignment col_j = SM_COLUMN_B(A,j) sets col_j to be a pointer to the diagonal element of the j-th column of the \(N \times N\) band matrix A, \(0 \le j \le N-1\). The type of the expression SM_COLUMN_B(A,j) is sunrealtype *. The pointer returned by the call SM_COLUMN_B(A,j) can be treated as an array which is indexed from -mu to ml.

Implementation:

#define SM_COLUMN_B(A,j)   ( ((SM_CONTENT_B(A)->cols)[j])+SM_SUBAND_B(A) )

SM_ELEMENT_B(A)

This macro gives access to the individual entries of the data array of a banded SUNMatrix.

The assignments SM_ELEMENT_B(A,i,j) = a_ij and a_ij = SM_ELEMENT_B(A,i,j) reference the (\(i,j\))-th element of the \(N \times N\) band matrix A, where \(0 \le i,j \le N-1\). The location (\(i,j\)) should further satisfy \(j-\text{mu} \le i \le j+\text{ml}\).

Implementation:

#define SM_ELEMENT_B(A,i,j)   ( (SM_CONTENT_B(A)->cols)[j][(i)-(j)+SM_SUBAND_B(A)] )

SM_COLUMN_ELEMENT_B(A)

This macro gives access to the individual entries of the data array of a banded SUNMatrix.

The assignments SM_COLUMN_ELEMENT_B(col_j,i,j) = a_ij and a_ij = SM_COLUMN_ELEMENT_B(col_j,i,j) reference the (\(i,j\))-th entry of the band matrix A when used in conjunction with SM_COLUMN_B to reference the j-th column through col_j. The index (\(i,j\)) should satisfy \(j-\text{mu} \le i \le j+\text{ml}\).

Implementation:

#define SM_COLUMN_ELEMENT_B(col_j,i,j)   (col_j[(i)-(j)])

The SUNMATRIX_BAND module defines banded implementations of all matrix operations listed in §10.2. Their names are obtained from those in that section by appending the suffix _Band (e.g. SUNMatCopy_Band). The module SUNMATRIX_BAND provides the following additional user-callable routines:

SUNMatrix SUNBandMatrix(sunindextype N, sunindextype mu, sunindextype ml, SUNContext sunctx): This constructor function creates and allocates memory for a banded SUNMatrix. Its arguments are the matrix size, N, and the upper and lower half-bandwidths of the matrix, mu and ml. The stored upper bandwidth is set to mu+ml to accommodate subsequent factorization in the SUNLINSOL_BAND and SUNLINSOL_LAPACKBAND modules.

SUNMatrix SUNBandMatrixStorage(sunindextype N, sunindextype mu, sunindextype ml, sunindextype smu, SUNContext sunctx)

This constructor function creates and allocates memory for a banded SUNMatrix. Its arguments are the matrix size, N, the upper and lower half-bandwidths of the matrix, mu and ml, and the stored upper bandwidth, smu. When creating a band SUNMatrix, this value should be

at least min(N-1,mu+ml) if the matrix will be used by the SUNLinSol_Band module;
exactly equal to mu+ml if the matrix will be used by the SUNLinSol_LapackBand module;
at least mu if used in some other manner.

Note

It is strongly recommended that users call the default constructor, SUNBandMatrix(), in all standard use cases. This advanced constructor is used internally within SUNDIALS solvers, and is provided to users who require banded matrices for non-default purposes.

void SUNBandMatrix_Print(SUNMatrix A, FILE *outfile): This function prints the content of a banded SUNMatrix to the output stream specified by outfile. Note: stdout or stderr may be used as arguments for outfile to print directly to standard output or standard error, respectively.

sunindextype SUNBandMatrix_Rows(SUNMatrix A): This function returns the number of rows in the banded SUNMatrix.

sunindextype SUNBandMatrix_Columns(SUNMatrix A): This function returns the number of columns in the banded SUNMatrix.

sunindextype SUNBandMatrix_LowerBandwidth(SUNMatrix A): This function returns the lower half-bandwidth for the banded SUNMatrix.

sunindextype SUNBandMatrix_UpperBandwidth(SUNMatrix A): This function returns the upper half-bandwidth of the banded SUNMatrix.

sunindextype SUNBandMatrix_StoredUpperBandwidth(SUNMatrix A): This function returns the stored upper half-bandwidth of the banded SUNMatrix.

sunindextype SUNBandMatrix_LDim(SUNMatrix A): This function returns the length of the leading dimension of the banded SUNMatrix.

sunindextype SUNBandMatrix_LData(SUNMatrix A): This function returns the length of the data array for the banded SUNMatrix.

sunrealtype *SUNBandMatrix_Data(SUNMatrix A): This function returns a pointer to the data array for the banded SUNMatrix.

sunrealtype **SUNBandMatrix_Cols(SUNMatrix A): This function returns a pointer to the cols array for the band SUNMatrix.

sunrealtype *SUNBandMatrix_Column(SUNMatrix A, sunindextype j): This function returns a pointer to the diagonal entry of the j-th column of the banded SUNMatrix. The resulting pointer should be indexed over the range -mu to ml.

Warning

When calling this function from the Fortran interfaces the shape of the array that is returned is [1], and the only element you can (legally) access is the diagonal element. Fortran users should instead work with the data array returned by SUNBandMatrix_Data() directly.

Notes

When looping over the components of a banded SUNMatrix A, the most efficient approaches are to:
- First obtain the component array via A_data = SUNBandMatrix_Data(A), or equivalently A_data = SM_DATA_B(A), and then access A_data[i] within the loop.
- First obtain the array of column pointers via A_cols = SUNBandMatrix_Cols(A), or equivalently A_cols = SM_COLS_B(A), and then access A_cols[j][i] within the loop.
- Within a loop over the columns, access the column pointer via A_colj = SUNBandMatrix_Column(A,j) and then to access the entries within that column using SM_COLUMN_ELEMENT_B(A_colj,i,j).
All three of these are more efficient than using SM_ELEMENT_B(A,i,j) within a double loop.
Within the SUNMatMatvec_Band routine, internal consistency checks are performed to ensure that the matrix is called with consistent N_Vector implementations. These are currently limited to: NVECTOR_SERIAL, NVECTOR_OPENMP, and NVECTOR_PTHREADS. As additional compatible vector implementations are added to SUNDIALS, these will be included within this compatibility check.

10.13. The SUNMATRIX_CUSPARSE Module

The SUNMATRIX_CUSPARSE module is an interface to the NVIDIA cuSPARSE matrix for use on NVIDIA GPUs [7]. All data stored by this matrix implementation resides on the GPU at all times.

The header file to be included when using this module is sunmatrix/sunmatrix_cusparse.h. The installed library to link to is libsundials_sunmatrixcusparse.lib where .lib is typically .so for shared libraries and .a for static libraries.

10.13.1. SUNMATRIX_CUSPARSE Description

The implementation currently supports the cuSPARSE CSR matrix format described in the cuSPARSE documentation, as well as a unique low-storage format for block-diagonal matrices of the form

\[\begin{split}\mathbf{A} = \begin{bmatrix} \mathbf{A_0} & 0 & \cdots & 0\\ 0 & \mathbf{A_2} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \mathbf{A_{n-1}}\\ \end{bmatrix},\end{split}\]

where all the block matrices \(\mathbf{A_j}\) share the same sparsity pattern. We will refer to this format as BCSR (not to be confused with the canonical BSR format where each block is stored as dense). In this format, the CSR column indices and row pointers are only stored for the first block and are computed only as necessary for other blocks. This can drastically reduce the amount of storage required compared to the regular CSR format when the number of blocks is large. This format is well-suited for, and intended to be used with, the SUNLinearSolver_cuSolverSp_batchQR linear solver (see §11.22).

The SUNMATRIX_CUSPARSE module is experimental and subject to change.

10.13.2. SUNMATRIX_CUSPARSE Functions

The SUNMATRIX_CUSPARSE module defines GPU-enabled sparse implementations of all matrix operations listed in §10.2 except for the SUNMatSpace() and SUNMatMatvecSetup() operations:

SUNMatGetID_cuSparse – returns SUNMATRIX_CUSPARSE
SUNMatClone_cuSparse
SUNMatDestroy_cuSparse
SUNMatZero_cuSparse
SUNMatCopy_cuSparse
SUNMatScaleAdd_cuSparse – performs \(A = cA + B\), where \(A\) and \(B\) must have the same sparsity pattern
SUNMatScaleAddI_cuSparse – performs \(A = cA + I\), where the diagonal of \(A\) must be present
SUNMatMatvec_cuSparse

In addition, the SUNMATRIX_CUSPARSE module defines the following implementation specific functions:

SUNMatrix SUNMatrix_cuSparse_NewCSR(int M, int N, int NNZ, cusparseHandle_t cusp, SUNContext sunctx): This constructor function creates and allocates memory for a SUNMATRIX_CUSPARSE SUNMatrix that uses the CSR storage format. Its arguments are the number of rows and columns of the matrix, M and N, the number of nonzeros to be stored in the matrix, NNZ, and a valid cusparseHandle_t.

SUNMatrix SUNMatrix_cuSparse_NewBlockCSR(int nblocks, int blockrows, int blockcols, int blocknnz, cusparseHandle_t cusp, SUNContext sunctx): This constructor function creates and allocates memory for a SUNMATRIX_CUSPARSE SUNMatrix object that leverages the SUNMAT_CUSPARSE_BCSR storage format to store a block diagonal matrix where each block shares the same sparsity pattern. The blocks must be square. The function arguments are the number of blocks, nblocks, the number of rows, blockrows, the number of columns, blockcols, the number of nonzeros in each each block, blocknnz, and a valid cusparseHandle_t.

Warning

The SUNMAT_CUSPARSE_BCSR format currently only supports square matrices, i.e., blockrows == blockcols.

SUNMatrix SUNMatrix_cuSparse_MakeCSR(cusparseMatDescr_t mat_descr, int M, int N, int NNZ, int *rowptrs, int *colind, sunrealtype *data, cusparseHandle_t cusp, SUNContext sunctx): This constructor function creates a SUNMATRIX_CUSPARSE SUNMatrix object from user provided pointers. Its arguments are a cusparseMatDescr_t that must have index base CUSPARSE_INDEX_BASE_ZERO, the number of rows and columns of the matrix, M and N, the number of nonzeros to be stored in the matrix, NNZ, and a valid cusparseHandle_t.

int SUNMatrix_cuSparse_Rows(SUNMatrix A): This function returns the number of rows in the sparse SUNMatrix.

int SUNMatrix_cuSparse_Columns(SUNMatrix A): This function returns the number of columns in the sparse SUNMatrix.

int SUNMatrix_cuSparse_NNZ(SUNMatrix A): This function returns the number of entries allocated for nonzero storage for the sparse SUNMatrix.

int SUNMatrix_cuSparse_SparseType(SUNMatrix A): This function returns the storage type (SUNMAT_CUSPARSE_CSR or SUNMAT_CUSPARSE_BCSR) for the sparse SUNMatrix.

sunrealtype *SUNMatrix_cuSparse_Data(SUNMatrix A): This function returns a pointer to the data array for the sparse SUNMatrix.

int *SUNMatrix_cuSparse_IndexValues(SUNMatrix A): This function returns a pointer to the index value array for the sparse SUNMatrix – for the CSR format this is an array of column indices for each nonzero entry. For the BCSR format this is an array of the column indices for each nonzero entry in the first block only.

int *SUNMatrix_cuSparse_IndexPointers(SUNMatrix A): This function returns a pointer to the index pointer array for the sparse SUNMatrix – for the CSR format this is an array of the locations of the first entry of each row in the data and indexvalues arrays, for the BCSR format this is an array of the locations of each row in the data and indexvalues arrays in the first block only.

int SUNMatrix_cuSparse_NumBlocks(SUNMatrix A): This function returns the number of matrix blocks.

int SUNMatrix_cuSparse_BlockRows(SUNMatrix A): This function returns the number of rows in a matrix block.

int SUNMatrix_cuSparse_BlockColumns(SUNMatrix A): This function returns the number of columns in a matrix block.

int SUNMatrix_cuSparse_BlockNNZ(SUNMatrix A): This function returns the number of nonzeros in each matrix block.

sunrealtype *SUNMatrix_cuSparse_BlockData(SUNMatrix A, int blockidx): This function returns a pointer to the location in the data array where the data for the block, blockidx, begins. Thus, blockidx must be less than SUNMatrix_cuSparse_NumBlocks(A). The first block in the SUNMatrix is index 0, the second block is index 1, and so on.

cusparseMatDescr_t SUNMatrix_cuSparse_MatDescr(SUNMatrix A): This function returns the cusparseMatDescr_t object associated with the matrix.

SUNErrCode SUNMatrix_cuSparse_CopyToDevice(SUNMatrix A, sunrealtype *h_data, int *h_idxptrs, int *h_idxvals)

This functions copies the matrix information to the GPU device from the provided host arrays. A user may provide NULL for any of h_data, h_idxptrs, or h_idxvals to avoid copying that information.

The function returns SUN_SUCCESS if the copy operation(s) were successful, or a nonzero error code otherwise.

SUNErrCode SUNMatrix_cuSparse_CopyFromDevice(SUNMatrix A, sunrealtype *h_data, int *h_idxptrs, int *h_idxvals)

This functions copies the matrix information from the GPU device to the provided host arrays. A user may provide NULL for any of h_data, h_idxptrs, or h_idxvals to avoid copying that information. Otherwise:

The h_data array must be at least SUNMatrix_cuSparse_NNZ(A)*sizeof(sunrealtype) bytes.
The h_idxptrs array must be at least (SUNMatrix_cuSparse_BlockDim(A)+1)*sizeof(int) bytes.
The h_idxvals array must be at least (SUNMatrix_cuSparse_BlockNNZ(A))*sizeof(int) bytes.

The function returns SUN_SUCCESS if the copy operation(s) were successful, or a nonzero error code otherwise.

SUNErrCode SUNMatrix_cuSparse_SetFixedPattern(SUNMatrix A, sunbooleantype yesno): This function changes the behavior of the the SUNMatZero operation on the object A. By default the matrix sparsity pattern is not considered to be fixed, thus, the SUNMatZero operation zeros out all data array as well as the indexvalues and indexpointers arrays. Providing a value of 1 or SUNTRUE for the yesno argument changes the behavior of SUNMatZero on A so that only the data is zeroed out, but not the indexvalues or indexpointers arrays. Providing a value of 0 or SUNFALSE for the yesno argument is equivalent to the default behavior.

SUNErrCode SUNMatrix_cuSparse_SetKernelExecPolicy(SUNMatrix A, SUNCudaExecPolicy *exec_policy): This function sets the execution policies which control the kernel parameters utilized when launching the CUDA kernels. By default the matrix is setup to use a policy which tries to leverage the structure of the matrix. See §9.15.2 for more information about the SUNCudaExecPolicy class.

10.13.3. SUNMATRIX_CUSPARSE Usage Notes

The SUNMATRIX_CUSPARSE module only supports 32-bit indexing, thus SUNDIALS must be built for 32-bit indexing to use this module.

The SUNMATRIX_CUSPARSE module can be used with CUDA streams by calling the cuSPARSE function cusparseSetStream on the cusparseHandle_t that is provided to the SUNMATRIX_CUSPARSE constructor.

Warning

When using the SUNMATRIX_CUSPARSE module with a SUNDIALS package (e.g. ARKODE), the stream given to cuSPARSE should be the same stream used for the NVECTOR object that is provided to the package, and the NVECTOR object given to the SUNMatvec operation. If different streams are utilized, synchronization issues may occur.

10.14. The SUNMATRIX_SPARSE Module

The sparse implementation of the SUNMatrix module, SUNMATRIX_SPARSE, is designed to work with either compressed-sparse-column (CSC) or compressed-sparse-row (CSR) sparse matrix formats. To this end, it defines the content field of SUNMatrix to be the following structure:

struct _SUNMatrixContent_Sparse {
  sunindextype M;
  sunindextype N;
  sunindextype NNZ;
  sunindextype NP;
  sunrealtype *data;
  int sparsetype;
  sunindextype *indexvals;
  sunindextype *indexptrs;
  /* CSC indices */
  sunindextype **rowvals;
  sunindextype **colptrs;
  /* CSR indices */
  sunindextype **colvals;
  sunindextype **rowptrs;
};

A diagram of the underlying data representation in a sparse matrix is shown in Fig. 10.2. A more complete description of the parts of this content field is given below:

M - number of rows
N - number of columns
NNZ - maximum number of nonzero entries in the matrix (allocated length of data and indexvals arrays)
NP - number of index pointers (e.g. number of column pointers for CSC matrix). For CSC matrices NP=N, and for CSR matrices NP=M. This value is set automatically at construction based the input choice for sparsetype.
data - pointer to a contiguous block of sunrealtype variables (of length NNZ), containing the values of the nonzero entries in the matrix
sparsetype - type of the sparse matrix (CSC_MAT or CSR_MAT)
indexvals - pointer to a contiguous block of int variables (of length NNZ), containing the row indices (if CSC) or column indices (if CSR) of each nonzero matrix entry held in data
indexptrs - pointer to a contiguous block of int variables (of length NP+1). For CSC matrices each entry provides the index of the first column entry into the data and indexvals arrays, e.g. if indexptr[3]=7, then the first nonzero entry in the fourth column of the matrix is located in data[7], and is located in row indexvals[7] of the matrix. The last entry contains the total number of nonzero values in the matrix and hence points one past the end of the active data in the data and indexvals arrays. For CSR matrices, each entry provides the index of the first row entry into the data and indexvals arrays.

The following pointers are added to the SUNMATRIX_SPARSE content structure for user convenience, to provide a more intuitive interface to the CSC and CSR sparse matrix data structures. They are set automatically when creating a sparse SUNMatrix, based on the sparse matrix storage type.

rowvals - pointer to indexvals when sparsetype is CSC_MAT, otherwise set to NULL.
colptrs - pointer to indexptrs when sparsetype is CSC_MAT, otherwise set to NULL.
colvals - pointer to indexvals when sparsetype is CSR_MAT, otherwise set to NULL.
rowptrs - pointer to indexptrs when sparsetype is CSR_MAT, otherwise set to NULL.

For example, the \(5\times 4\) matrix

\[\begin{split}\left[\begin{array}{cccc} 0 & 3 & 1 & 0\\ 3 & 0 & 0 & 2\\ 0 & 7 & 0 & 0\\ 1 & 0 & 0 & 9\\ 0 & 0 & 0 & 5 \end{array}\right]\end{split}\]

could be stored as a CSC matrix in this structure as either

M = 5;
N = 4;
NNZ = 8;
NP = N;
data = {3.0, 1.0, 3.0, 7.0, 1.0, 2.0, 9.0, 5.0};
sparsetype = CSC_MAT;
indexvals = {1, 3, 0, 2, 0, 1, 3, 4};
indexptrs = {0, 2, 4, 5, 8};

or

M = 5;
N = 4;
NNZ = 10;
NP = N;
data = {3.0, 1.0, 3.0, 7.0, 1.0, 2.0, 9.0, 5.0, *, *};
sparsetype = CSC_MAT;
indexvals = {1, 3, 0, 2, 0, 1, 3, 4, *, *};
indexptrs = {0, 2, 4, 5, 8};

where the first has no unused space, and the second has additional storage (the entries marked with * may contain any values). Note in both cases that the final value in indexptrs is 8, indicating the total number of nonzero entries in the matrix.

Similarly, in CSR format, the same matrix could be stored as

M = 5;
N = 4;
NNZ = 8;
NP = M;
data = {3.0, 1.0, 3.0, 2.0, 7.0, 1.0, 9.0, 5.0};
sparsetype = CSR_MAT;
indexvals = {1, 2, 0, 3, 1, 0, 3, 3};
indexptrs = {0, 2, 4, 5, 7, 8};

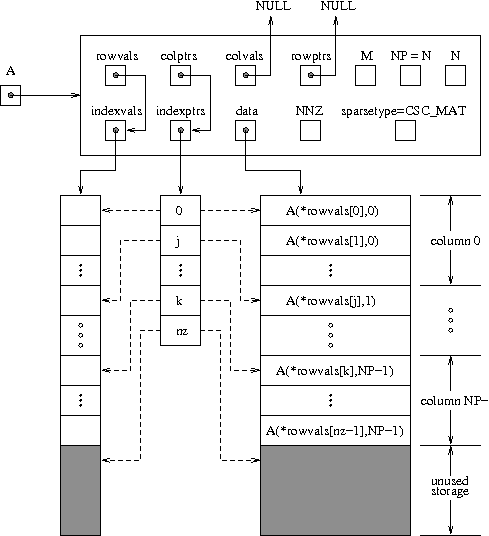
../_images/cscmat.png — Fig. 10.2 Diagram of the storage for a compressed-sparse-column matrix of type SUNMATRIX_SPARSE: Here `A` is an \(M \times N\) sparse CSC matrix with storage for up to `NNZ` nonzero entries (the allocated length of both `data` and `indexvals`). The entries in `indexvals` may assume values from `0` to `M-1`, corresponding to the row index (zero-based) of each nonzero value. The entries in `data` contain the values of the nonzero entries, with the row `i`, column `j` entry of `A` (again, zero-based) denoted as `A(i,j)`. The `indexptrs` array contains `N+1` entries; the first `N` denote the starting index of each column within the `indexvals` and `data` arrays, while the final entry points one past the final nonzero entry. Here, although `NNZ` values are allocated, only `nz` are actually filled in; the greyed-out portions of `data` and `indexvals` indicate extra allocated space.

The header file to be included when using this module is sunmatrix/sunmatrix_sparse.h.

The following macros are provided to access the content of a SUNMATRIX_SPARSE matrix. The prefix SM_ in the names denotes that these macros are for SUNMatrix implementations, and the suffix _S denotes that these are specific to the sparse version.

SM_CONTENT_S(A)

This macro gives access to the contents of the sparse SUNMatrix A.

The assignment A_cont = SM_CONTENT_S(A) sets A_cont to be a pointer to the sparse SUNMatrix content structure.

Implementation:

#define SM_CONTENT_S(A)   ( (SUNMatrixContent_Sparse)(A->content) )

SM_ROWS_S(A)

Access the number of rows in the sparse SUNMatrix A.

This may be used either to retrieve or to set the value. For example, the assignment A_rows = SM_ROWS_S(A) sets A_rows to be the number of rows in the matrix A. Similarly, the assignment SM_ROWS_S(A) = A_rows sets the number of columns in A to equal A_rows.

Implementation:

#define SM_ROWS_S(A)   ( SM_CONTENT_S(A)->M )

SM_COLUMNS_S(A)

Access the number of columns in the sparse SUNMatrix A. As with SM_ROWS_S, this may be used either to retrieve or to set the value.

Implementation:

#define SM_COLUMNS_S(A)   ( SM_CONTENT_S(A)->N )

SM_NNZ_S(A)

Access the allocated number of nonzeros in the sparse SUNMatrix A. As with SM_ROWS_S, this may be used either to retrieve or to set the value.

Implementation:

#define SM_NNZ_S(A)   ( SM_CONTENT_S(A)->NNZ )

SM_NP_S(A)

Access the number of index pointers NP in the sparse SUNMatrix A. As with SM_ROWS_S, this may be used either to retrieve or to set the value.

Implementation:

#define SM_NP_S(A)   ( SM_CONTENT_S(A)->NP )

SM_SPARSETYPE_S(A)

Access the sparsity type parameter in the sparse SUNMatrix A. As with SM_ROWS_S, this may be used either to retrieve or to set the value.

Implementation:

#define SM_SPARSETYPE_S(A)   ( SM_CONTENT_S(A)->sparsetype )

SM_DATA_S(A)

This macro gives access to the data pointer for the matrix entries.

The assignment A_data = SM_DATA_S(A) sets A_data to be a pointer to the first component of the data array for the sparse SUNMatrix A. The assignment SM_DATA_S(A) = A_data sets the data array of A to be A_data by storing the pointer A_data.

Implementation:

#define SM_DATA_S(A)   ( SM_CONTENT_S(A)->data )

SM_INDEXVALS_S(A)

This macro gives access to the indexvals pointer for the matrix entries.

The assignment A_indexvals = SM_INDEXVALS_S(A) sets A_indexvals to be a pointer to the array of index values (i.e. row indices for a CSC matrix, or column indices for a CSR matrix) for the sparse SUNMatrix A.

Implementation:

#define SM_INDEXVALS_S(A)   ( SM_CONTENT_S(A)->indexvals )

SM_INDEXPTRS_S(A)

This macro gives access to the indexptrs pointer for the matrix entries.

The assignment A_indexptrs = SM_INDEXPTRS_S(A) sets A_indexptrs to be a pointer to the array of index pointers (i.e. the starting indices in the data/indexvals arrays for each row or column in CSR or CSC formats, respectively).

Implementation:

#define SM_INDEXPTRS_S(A)   ( SM_CONTENT_S(A)->indexptrs )

The SUNMATRIX_SPARSE module defines sparse implementations of all matrix operations listed in §10.2. Their names are obtained from those in that section by appending the suffix _Sparse (e.g. SUNMatCopy_Sparse). The module SUNMATRIX_SPARSE provides the following additional user-callable routines:

SUNMatrix SUNSparseMatrix(sunindextype M, sunindextype N, sunindextype NNZ, int sparsetype, SUNContext sunctx): This constructor function creates and allocates memory for a sparse SUNMatrix. Its arguments are the number of rows and columns of the matrix, M and N, the maximum number of nonzeros to be stored in the matrix, NNZ, and a flag sparsetype indicating whether to use CSR or CSC format (valid choices are CSR_MAT or CSC_MAT).

SUNMatrix SUNSparseFromDenseMatrix(SUNMatrix A, sunrealtype droptol, int sparsetype)

This constructor function creates a new sparse matrix from an existing SUNMATRIX_DENSE object by copying all values with magnitude larger than droptol into the sparse matrix structure.

Requirements:

A must have type SUNMATRIX_DENSE
droptol must be non-negative
sparsetype must be either CSC_MAT or CSR_MAT

The function returns NULL if any requirements are violated, or if the matrix storage request cannot be satisfied.

SUNMatrix SUNSparseFromBandMatrix(SUNMatrix A, sunrealtype droptol, int sparsetype)

This constructor function creates a new sparse matrix from an existing SUNMATRIX_BAND object by copying all values with magnitude larger than droptol into the sparse matrix structure.

Requirements:

A must have type SUNMATRIX_BAND
droptol must be non-negative
sparsetype must be either CSC_MAT or CSR_MAT.

The function returns NULL if any requirements are violated, or if the matrix storage request cannot be satisfied.

SUNErrCode SUNSparseMatrix_Realloc(SUNMatrix A): This function reallocates internal storage arrays in a sparse matrix so that the resulting sparse matrix has no wasted space (i.e. the space allocated for nonzero entries equals the actual number of nonzeros, indexptrs[NP]). Returns a SUNErrCode.

SUNErrCode SUNSparseMatrix_Reallocate(SUNMatrix A): Function to reallocate internal sparse matrix storage arrays so that the resulting sparse matrix has storage for a specified number of nonzeros. Returns a SUNErrCode.

void SUNSparseMatrix_Print(SUNMatrix A, FILE *outfile): This function prints the content of a sparse SUNMatrix to the output stream specified by outfile. Note: stdout or stderr may be used as arguments for outfile to print directly to standard output or standard error, respectively.

sunindextype SUNSparseMatrix_Rows(SUNMatrix A): This function returns the number of rows in the sparse SUNMatrix.

sunindextype SUNSparseMatrix_Columns(SUNMatrix A): This function returns the number of columns in the sparse SUNMatrix.

sunindextype SUNSparseMatrix_NNZ(SUNMatrix A): This function returns the number of entries allocated for nonzero storage for the sparse SUNMatrix.

sunindextype SUNSparseMatrix_NP(SUNMatrix A): This function returns the number of index pointers for the sparse SUNMatrix (the indexptrs array has NP+1 entries).

int SUNSparseMatrix_SparseType(SUNMatrix A): This function returns the storage type (CSR_MAT or CSC_MAT) for the sparse SUNMatrix.

sunrealtype *SUNSparseMatrix_Data(SUNMatrix A): This function returns a pointer to the data array for the sparse SUNMatrix.

sunindextype *SUNSparseMatrix_IndexValues(SUNMatrix A): This function returns a pointer to index value array for the sparse SUNMatrix – for CSR format this is the column index for each nonzero entry, for CSC format this is the row index for each nonzero entry.

sunindextype *SUNSparseMatrix_IndexPointers(SUNMatrix A): This function returns a pointer to the index pointer array for the sparse SUNMatrix – for CSR format this is the location of the first entry of each row in the data and indexvalues arrays, for CSC format this is the location of the first entry of each column.

Note

Within the SUNMatMatvec_Sparse routine, internal consistency checks are performed to ensure that the matrix is called with consistent N_Vector implementations. These are currently limited to: NVECTOR_SERIAL, NVECTOR_OPENMP, NVECTOR_PTHREADS, and NVECTOR_CUDA when using managed memory. As additional compatible vector implementations are added to SUNDIALS, these will be included within this compatibility check.

10.15. The SUNMATRIX_SLUNRLOC Module

The SUNMATRIX_SLUNRLOC module is an interface to the SuperMatrix structure provided by the SuperLU_DIST sparse matrix factorization and solver library written by X. Sherry Li and collaborators [8, 57, 89, 90]. It is designed to be used with the SuperLU_DIST SUNLinearSolver module discussed in §11.20. To this end, it defines the content field of SUNMatrix to be the following structure:

struct _SUNMatrixContent_SLUNRloc {
  sunbooleantype own_data;
  gridinfo_t    *grid;
  sunindextype  *row_to_proc;
  pdgsmv_comm_t *gsmv_comm;
  SuperMatrix   *A_super;
  SuperMatrix   *ACS_super;
};

A more complete description of the this content field is given below:

own_data – a flag which indicates if the SUNMatrix is responsible for freeing A_super
grid – pointer to the SuperLU_DIST structure that stores the 2D process grid
row_to_proc – a mapping between the rows in the matrix and the process it resides on; will be NULL until the SUNMatMatvecSetup routine is called
gsmv_comm – pointer to the SuperLU_DIST structure that stores the communication information needed for matrix-vector multiplication; will be NULL until the SUNMatMatvecSetup routine is called
A_super – pointer to the underlying SuperLU_DIST SuperMatrix with Stype = SLU_NR_loc, Dtype = SLU_D, Mtype = SLU_GE; must have the full diagonal present to be used with SUNMatScaleAddI routine
ACS_super – a column-sorted version of the matrix needed to perform matrix-vector multiplication; will be NULL until the routine SUNMatMatvecSetup routine is called

The header file to include when using this module is sunmatrix/sunmatrix_slunrloc.h. The installed module library to link to is libsundials_sunmatrixslunrloc .lib where .lib is typically .so for shared libraries and .a for static libraries.

10.15.1. SUNMATRIX_SLUNRLOC Functions

The SUNMATRIX_SLUNRLOC module provides the following user-callable routines:

SUNMatrix SUNMatrix_SLUNRloc(SuperMatrix *Asuper, gridinfo_t *grid, SUNContext sunctx): This constructor function creates and allocates memory for a SUNMATRIX_SLUNRLOC object. Its arguments are a fully-allocated SuperLU_DIST SuperMatrix with Stype = SLU_NR_loc, Dtype = SLU_D, Mtype = SLU_GE and an initialized SuperLU_DIST 2D process grid structure. It returns a SUNMatrix object if Asuper is compatible else it returns NULL.

void SUNMatrix_SLUNRloc_Print(SUNMatrix A, FILE *fp): This function prints the underlying SuperMatrix content. It is useful for debugging. Its arguments are the SUNMatrix object and a FILE pointer to print to. It returns void.

SuperMatrix *SUNMatrix_SLUNRloc_SuperMatrix(SUNMatrix A): This function returns the underlying SuperMatrix of A. Its only argument is the SUNMatrix object to access.

gridinfo_t *SUNMatrix_SLUNRloc_ProcessGrid(SUNMatrix A): This function returns the SuperLU_DIST 2D process grid associated with A. Its only argument is the SUNMatrix object to access.

sunbooleantype SUNMatrix_SLUNRloc_OwnData(SUNMatrix A): This function returns true if the SUNMatrix object is responsible for freeing the underlying SuperMatrix, otherwise it returns false. Its only argument is the SUNMatrix object to access.

The SUNMATRIX_SLUNRLOC module also defines implementations of all generic SUNMatrix operations listed in §10.2:

SUNMatGetID_SLUNRloc – returns SUNMATRIX_SLUNRLOC
SUNMatClone_SLUNRloc
SUNMatDestroy_SLUNRloc
SUNMatSpace_SLUNRloc – this only returns information for the storage within the matrix interface, i.e. storage for row_to_proc
SUNMatZero_SLUNRloc
SUNMatCopy_SLUNRloc
SUNMatScaleAdd_SLUNRloc – performs \(A = cA + B\), where \(A\) and \(B\) must have the same sparsity pattern
SUNMatScaleAddI_SLUNRloc – performs \(A = cA + I\), where the diagonal of \(A\) must be present
SUNMatMatvecSetup_SLUNRloc – initializes the SuperLU_DIST parallel communication structures needed to perform a matrix-vector product; only needs to be called before the first call to SUNMatMatvec() or if the matrix changed since the last setup
SUNMatMatvec_SLUNRloc

10.16. The SUNMATRIX_GINKGO Module

New in version 6.4.0.

The SUNMATRIX_GINKGO implementation of the SUNMatrix API provides an interface to the matrix data structure for the Ginkgo linear algebra library [12]. Ginkgo provides several different matrix formats and linear solvers which can run on a variety of hardware, such as NVIDIA, AMD, and Intel GPUs as well as multicore CPUs. Since Ginkgo is a modern C++ library, SUNMATRIX_GINKGO is also written in modern C++ (it requires C++14). Unlike most other SUNDIALS modules, it is a header only library. To use the SUNMATRIX_GINKGO SUNMatrix, users will need to include sunmatrix/sunmatrix_ginkgo.hpp. More instructions on building SUNDIALS with Ginkgo enabled are given in §2.2.4. For instructions on building and using Ginkgo itself, refer to the Ginkgo website and documentation.

Note

It is assumed that users of this module are aware of how to use Ginkgo. This module does not try to encapsulate Ginkgo matrices, rather it provides a lightweight iteroperability layer between Ginkgo and SUNDIALS.

The SUNMATRIX_GINKGO module is defined by the sundials::ginkgo::Matrix templated class:

template<typename GkoMatType>
class Matrix : public sundials::impl::BaseMatrix, public sundials::ConvertibleTo<SUNMatrix>;

10.16.1. Compatible `N_Vectors`

The N_Vector to use with the SUNLINEARSOLVER_GINKGO module depends on the gko::Executor utilized. That is, when using the gko::CudaExecutor you should use a CUDA capable N_Vector (e.g., §9.15), gko::HipExecutor goes with a HIP capable N_Vector (e.g., §9.16), gko::DpcppExecutor goes with a DPC++/SYCL capable N_Vector (e.g., §9.17), and gko::OmpExecutor goes with a CPU based N_Vector (e.g., §9.11). Specifically, what makes a N_Vector compatible with different Ginkgo executors is where they store the data. The GPU enabled Ginkgo executors need the data to reside on the GPU, so the N_Vector must implement N_VGetDeviceArrayPointer() and keep the data in GPU memory. The CPU-only enabled Ginkgo executors (e.g, gko::OmpExecutor and gko::ReferenceExecutor) need data to reside on the CPU and will use N_VGetArraryPointer() to access the N_Vector data.

10.16.2. Using SUNMATRIX_GINKGO

To use the SUNMATRIX_GINKGO module, we begin by creating an instance of a Ginkgo matrix using Ginkgo’s API. For example, below we create a Ginkgo sparse matrix that uses the CSR storage format and then fill the diagonal of the matrix with ones to make an identity matrix:

auto gko_matrix{gko::matrix::Csr<sunrealtype, sunindextype>::create(gko_exec, matrix_dim)};
gko_matrix->read(gko::matrix_data<sunrealtype, sunindextype>::diag(matrix_dim, 1.0));

After we have a Ginkgo matrix object, we wrap it in an instance of the sundials::ginkgo::Matrix class. This object can be provided to other SUNDIALS functions that expect a SUNMatrix object via implicit conversion, or the Convert() method:

sundials::ginkgo::Matrix<gko::matrix::Csr> matrix{gko_matrix, sunctx};
SUNMatrix I1 = matrix.Convert(); // explicit conversion to SUNMatrix
SUNMatrix I2 = matrix;  // implicit conversion to SUNMatrix

No further interaction with matrix is required from this point, and it is possible to to use the SUNMatrix API operating on I1 or I2 (or if needed, via Ginkgo operations on gko_matrix).

Warning

SUNMatDestroy() should never be called on a SUNMatrix that was created via conversion from a sundials::ginkgo::Matrix. Doing so may result in a double free.

10.16.3. SUNMATRIX_GINKGO API

In this section we list the public API of the sundials::ginkgo::Matrix class.

template<typename GkoMatType> class Matrix : public sundials::impl::BaseMatrix, public sundials::ConvertibleTo<SUNMatrix>

Matrix() = default: Default constructor - means the matrix must be copied or moved to.

Matrix(std::shared_ptr<GkoMatType> gko_mat, SUNContext sunctx)

Constructs a Matrix from an existing Ginkgo matrix object.

Parameters:

gko_mat – A Ginkgo matrix object
sunctx – The SUNDIALS simulation context object (SUNContext)

Matrix(Matrix &&that_matrix) noexcept: Move constructor.

Matrix(const Matrix &that_matrix): Copy constructor (performs a deep copy).

Matrix &operator=(Matrix &&rhs) noexcept: Move assignment.

Matrix &operator=(const Matrix &rhs): Copy assignment clones the gko::matrix and SUNMatrix. This is a deep copy (i.e. a new data array is created).

virtual ~Matrix() = default;: Default destructor.

std::shared_ptr<GkoMatType> GkoMtx() const: Get the underlying Ginkgo matrix object.

std::shared_ptr<const gko::Executor> GkoExec() const: Get the gko::Executor associated with the Ginkgo matrix.

const gko::dim<2> &GkoSize() const: Get the size, i.e. gko::dim, for the Ginkgo matrix.

operator SUNMatrix() override: Implicit conversion to a SUNMatrix.

operator SUNMatrix() const override: Implicit conversion to a SUNMatrix.

SUNMatrix Convert() override: Explicit conversion to a SUNMatrix.

SUNMatrix Convert() const override: Explicit conversion to a SUNMatrix.

10.17. The SUNMATRIX_KOKKOSDENSE Module

New in version 6.4.0.

The SUNMATRIX_KOKKOSDENSE SUNMatrix implementation provides a data structure for dense and dense batched (block-diagonal) matrices using Kokkos [47, 124] and KokkosKernels [123] to support a variety of backends including serial, OpenMP, CUDA, HIP, and SYCL. Since Kokkos is a modern C++ library, the module is also written in modern C++ (it requires C++14) as a header only library. To utilize this SUNMatrix users will need to include sunmatrix/sunmatrix_kokkosdense.hpp. More instructions on building SUNDIALS with Kokkos and KokkosKernels enabled are given in §2.2.4. For instructions on building and using Kokkos and KokkosKernels, refer to the Kokkos and KokkosKernels. documentation.

10.17.1. Using SUNMATRIX_KOKKOSDENSE

The SUNMATRIX_KOKKOSDENSE module is defined by the DenseMatrix templated class in the sundials::kokkos namespace:

template<class ExecutionSpace = Kokkos::DefaultExecutionSpace,
         class MemorySpace = typename ExecSpace::memory_space>
class DenseMatrix : public sundials::impl::BaseMatrix,
                    public sundials::ConvertibleTo<SUNMatrix>

To use the SUNMATRIX_KOKKOSDENSE module, we begin by constructing an instance of the Kokkos dense matrix e.g.,

// Single matrix using the default execution space
sundials::kokkos::DenseMatrix<> A{rows, cols, sunctx};

// Batched (block-diagonal) matrix using the default execution space
sundials::kokkos::DenseMatrix<> Abatch{blocks, rows, cols, sunctx};

// Batched (block-diagonal) matrix using the Cuda execution space
sundials::kokkos::DenseMatrix<Kokkos::Cuda> Abatch{blocks, rows, cols, sunctx};

// Batched (block-diagonal) matrix using the Cuda execution space and
// a non-default execution space instance
sundials::kokkos::DenseMatrix<Kokkos::Cuda> Abatch{blocks, rows, cols,
                                                   exec_space_instance,
                                                   sunctx};

Instances of the DenseMatrix class are implicitly or explicitly (using the Convert() method) convertible to a SUNMatrix e.g.,

sundials::kokkos::DenseMatrix<> A{rows, cols, sunctx};
SUNMatrix B = A;           // implicit conversion to SUNMatrix
SUNMatrix C = A.Convert(); // explicit conversion to SUNMatrix

No further interaction with a DenseMatrix is required from this point, and it is possible to use the SUNMatrix API to operate on B or C.

Warning

SUNMatDestroy() should never be called on a SUNMatrix that was created via conversion from a sundials::kokkos::DenseMatrix. Doing so may result in a double free.

The underlying DenseMatrix can be extracted from a SUNMatrix using GetDenseMat() e.g.,

auto A_dense_mat = GetDenseMat<>(A_sunmat);

The SUNMATRIX_KOKKOSDENSE module is compatible with the NVECTOR_KOKKOS vector module (see §9.19) and SUNLINEARSOLVER_KOKKOSDENSE linear solver module (see §11.24).

10.17.2. SUNMATRIX_KOKKOSDENSE API

In this section we list the public API of the sundials::kokkos::DenseMatrix class.

template<class ExeccutionSpace = Kokkos::DefaultExecutionSpace, class MemorySpace = typename ExecSpace::memory_space> class DenseMatrix : public sundials::impl::BaseMatrix, public sundials::ConvertibleTo<SUNMatrix>

DenseMatrix() = default: Default constructor – the matrix must be copied or moved to.

DenseMatrix(size_type rows, size_type cols, SUNContext sunctx)

Constructs a single DenseMatrix using the default execution space instance.

Parameters:

rows – number of matrix rows
cols – number of matrix columns
sunctx – the SUNDIALS simulation context object (SUNContext)

DenseMatrix(size_type rows, size_type cols, exec_space ex, SUNContext sunctx)

Constructs a single DenseMatrix using the provided execution space instance.

Parameters:

rows – number of matrix rows
cols – number of matrix columns
exec_space – a ExecSpace instance
sunctx – the SUNDIALS simulation context object (SUNContext)

DenseMatrix(size_type blocks, size_type block_rows, size_type block_cols, SUNContext sunctx)

Constructs a batched (block-diagonal) DenseMatrix using the default execution space instance.

Parameters:

blocks – number of matrix blocks
block_rows – number of rows in a block
block_cols – number of columns in a block
sunctx – the SUNDIALS simulation context object (SUNContext)

DenseMatrix(size_type blocks, size_type block_rows, size_type block_cols, exec_space ex, SUNContext sunctx)

Constructs a batched (block-diagonal) DenseMatrix using the provided execution space instance.

Parameters:

blocks – number of matrix blocks
block_rows – number of rows in a block
block_cols – number of columns in a block
exec_space – a ExecSpace instance
sunctx – the SUNDIALS simulation context object (SUNContext)

DenseMatrix(DenseMatrix &&that_matrix) noexcept: Move constructor.

DenseMatrix(const DenseMatrix &that_matrix): Copy constructor. This creates a shallow clone of the Matrix, i.e., it creates a new Matrix with the same properties, such as size, but it does not copy the data.

DenseMatrix &operator=(DenseMatrix &&rhs) noexcept: Move assignment.

DenseMatrix &operator=(const DenseMatrix &rhs): Copy assignment. This creates a shallow clone of the Matrix, i.e., it creates a new Matrix with the same properties, such as size, but it does not copy the data.

virtual ~DenseMatrix() = default;: Default destructor.

exec_space ExecSpace(): Get the execution space instance used by the matrix.

view_type View(): Get the underlying Kokkos view with extents {blocks, block_rows, block_cols}.

size_type Blocks(): Get the number of blocks i.e., extent(0).

size_type BlockRows(): Get the number of rows in a block i.e., extent(1).

size_type BlockCols(): Get the number of columns in a block i.e., extent(2).

size_type Rows(): Get the number of rows in the block-diagonal matrix i.e., extent(0) * extent(1).

size_type Cols(): Get the number of columns in the block-diagonal matrix i.e., extent(0) * extent(2).

operator SUNMatrix() override: Implicit conversion to a SUNMatrix.

operator SUNMatrix() const override: Implicit conversion to a SUNMatrix.

SUNMatrix Convert() override: Explicit conversion to a SUNMatrix.

SUNMatrix Convert() const override: Explicit conversion to a SUNMatrix.

template<class ExecutionSpace = Kokkos::DefaultExecutionSpace, class MemorySpace = typename ExecSpace::memory_space> inline DenseMatrix<MatrixType> *GetDenseMat(SUNMatrix A): Get the dense matrix wrapped by a SUNMatrix

10.18. SUNMATRIX Examples

There are SUNMatrix examples that may be installed for each implementation, that make use of the functions in test_sunmatrix.c. These example functions show simple usage of the SUNMatrix family of functions. The inputs to the examples depend on the matrix type, and are output to stdout if the example is run without the appropriate number of command-line arguments.

The following is a list of the example functions in test_sunmatrix.c:

Test_SUNMatGetID: Verifies the returned matrix ID against the value that should be returned.
Test_SUNMatClone: Creates clone of an existing matrix, copies the data, and checks that their values match.
Test_SUNMatZero: Zeros out an existing matrix and checks that each entry equals 0.0.
Test_SUNMatCopy: Clones an input matrix, copies its data to a clone, and verifies that all values match.
Test_SUNMatScaleAdd: Given an input matrix \(A\) and an input identity matrix \(I\), this test clones and copies \(A\) to a new matrix \(B\), computes \(B = -B+B\), and verifies that the resulting matrix entries equal 0. Additionally, if the matrix is square, this test clones and copies \(A\) to a new matrix \(D\), clones and copies \(I\) to a new matrix \(C\), computes \(D = D+I\) and \(C = C+A\) using SUNMatScaleAdd(), and then verifies that \(C=D\).
Test_SUNMatScaleAddI: Given an input matrix \(A\) and an input identity matrix \(I\), this clones and copies \(I\) to a new matrix \(B\), computes \(B = -B+I\) using SUNMatScaleAddI(), and verifies that the resulting matrix entries equal 0.
Test_SUNMatMatvecSetup: verifies that SUNMatMatvecSetup() can be called.
Test_SUNMatMatvec Given an input matrix \(A\) and input vectors \(x\) and \(y\) such that \(y=Ax\), this test has different behavior depending on whether \(A\) is square. If it is square, it clones and copies \(A\) to a new matrix \(B\), computes \(B = 3B+I\) using SUNMatScaleAddI(), clones \(y\) to new vectors \(w\) and \(z\), computes \(z = Bx\) using SUNMatMatvec(), computes \(w = 3y+x\) using N_VLinearSum, and verifies that \(w==z\). If \(A\) is not square, it just clones \(y\) to a new vector \(z\), computes :math:`z=Ax using SUNMatMatvec(), and verifies that \(y=z\).
Test_SUNMatSpace: verifies that SUNMatSpace() can be called, and outputs the results to stdout.

10.9. The SUNMATRIX_DENSE Module

10.10. The SUNMATRIX_MAGMADENSE Module

10.10.1. SUNMATRIX_MAGMADENSE Functions

10.10.2. SUNMATRIX_MAGMADENSE Usage Notes

10.11. The SUNMATRIX_ONEMKLDENSE Module

10.11.1. SUNMATRIX_ONEMKLDENSE Functions

10.11.1.1. Constructors

10.11.1.2. Access Matrix Dimensions

10.11.1.3. Access Matrix Block Dimensions

10.11.1.4. Access Matrix Data

10.11.1.5. Access Matrix Block Data

10.11.1.6. Copy Data

10.11.2. SUNMATRIX_ONEMKLDENSE Usage Notes

10.12. The SUNMATRIX_BAND Module

10.13. The SUNMATRIX_CUSPARSE Module

10.13.1. SUNMATRIX_CUSPARSE Description

10.13.2. SUNMATRIX_CUSPARSE Functions

10.13.3. SUNMATRIX_CUSPARSE Usage Notes

10.14. The SUNMATRIX_SPARSE Module

10.15. The SUNMATRIX_SLUNRLOC Module

10.15.1. SUNMATRIX_SLUNRLOC Functions

10.16. The SUNMATRIX_GINKGO Module

10.16.1. Compatible N_Vectors

10.16.2. Using SUNMATRIX_GINKGO

10.16.3. SUNMATRIX_GINKGO API

10.17. The SUNMATRIX_KOKKOSDENSE Module

10.17.1. Using SUNMATRIX_KOKKOSDENSE

10.17.2. SUNMATRIX_KOKKOSDENSE API

10.18. SUNMATRIX Examples

10.16.1. Compatible `N_Vectors`