3.2. Mathematical Considerations
ARKODE solves ODE initial value problems (IVP) in \(\mathbb{R}^N\) posed in the form
Here, \(t\) is the independent variable (e.g. time), and the dependent variables are given by \(y \in \mathbb{R}^N\), where we use the notation \(\dot{y}\) to denote \(\mathrm dy/\mathrm dt\).
For each value of \(t\), \(M(t)\) is a user-specified linear operator from \(\mathbb{R}^N \to \mathbb{R}^N\). This operator is assumed to be nonsingular and independent of \(y\). For standard systems of ordinary differential equations and for problems arising from the spatial semi-discretization of partial differential equations using finite difference, finite volume, or spectral finite element methods, \(M\) is typically the identity matrix, \(I\). For PDEs using standard finite-element spatial semi-discretizations, \(M\) is typically a well-conditioned mass matrix that is fixed throughout a simulation (or at least fixed between spatial rediscretization events).
The ODE right-hand side is given by the function \(f(t,y)\) – in general we make no assumption that the problem (3.5) is autonomous (i.e., \(f=f(y)\)) or linear (\(f=Ay\)). In general, the time integration methods within ARKODE support additive splittings of this right-hand side function, as described in the subsections that follow. Through these splittings, the time-stepping methods currently supplied with ARKODE are designed to solve stiff, nonstiff, mixed stiff/nonstiff, and multirate problems. As per Ascher and Petzold [13], a problem is “stiff” if the stepsize needed to maintain stability of the forward Euler method is much smaller than that required to represent the solution accurately.
In the sub-sections that follow, we elaborate on the numerical methods utilized in ARKODE. We first discuss the “single-step” nature of the ARKODE infrastructure, including its usage modes and approaches for interpolated solution output. We then discuss the current suite of time-stepping modules supplied with ARKODE, including the ARKStep module for additive Runge–Kutta methods, the ERKStep module that is optimized for explicit Runge–Kutta methods, and the MRIStep module for multirate infinitesimal step (MIS), multirate infinitesimal GARK (MRI-GARK), and implicit-explicit MRI-GARK (IMEX-MRI-GARK) methods. We then discuss the adaptive temporal error controllers shared by the time-stepping modules, including discussion of our choice of norms for measuring errors within various components of the solver.
We then discuss the nonlinear and linear solver strategies used by ARKODE’s time-stepping modules for solving implicit algebraic systems that arise in computing each stage and/or step: nonlinear solvers, linear solvers, preconditioners, error control within iterative nonlinear and linear solvers, algorithms for initial predictors for implicit stage solutions, and approaches for handling non-identity mass-matrices.
We conclude with a section describing ARKODE’s rootfinding capabilities, that may be used to stop integration of a problem prematurely based on traversal of roots in user-specified functions.
3.2.1. Adaptive single-step methods
The ARKODE infrastructure is designed to support single-step, IVP integration methods, i.e.
where \(y_{n-1}\) is an approximation to the solution \(y(t_{n-1})\), \(y_{n}\) is an approximation to the solution \(y(t_n)\), \(t_n = t_{n-1} + h_n\), and the approximation method is represented by the function \(\varphi\).
The choice of step size \(h_n\) is determined by the time-stepping method (based on user-provided inputs, typically accuracy requirements). However, users may place minimum/maximum bounds on \(h_n\) if desired.
ARKODE’s time stepping modules may be run in a variety of “modes”:
NORMAL – The solver will take internal steps until it has just overtaken a user-specified output time, \(t_\text{out}\), in the direction of integration, i.e. \(t_{n-1} < t_\text{out} \le t_{n}\) for forward integration, or \(t_{n} \le t_\text{out} < t_{n-1}\) for backward integration. It will then compute an approximation to the solution \(y(t_\text{out})\) by interpolation (using one of the dense output routines described in the section §3.2.2).
ONE-STEP – The solver will only take a single internal step \(y_{n-1} \to y_{n}\) and then return control back to the calling program. If this step will overtake \(t_\text{out}\) then the solver will again return an interpolated result; otherwise it will return a copy of the internal solution \(y_{n}\).
NORMAL-TSTOP – The solver will take internal steps until the next step will overtake \(t_\text{out}\). It will then limit this next step so that \(t_n = t_{n-1} + h_n = t_\text{out}\), and once the step completes it will return a copy of the internal solution \(y_{n}\).
ONE-STEP-TSTOP – The solver will check whether the next step will overtake \(t_\text{out}\) – if not then this mode is identical to “one-step” above; otherwise it will limit this next step so that \(t_n = t_{n-1} + h_n = t_\text{out}\). In either case, once the step completes it will return a copy of the internal solution \(y_{n}\).
We note that interpolated solutions may be slightly less accurate than the internal solutions produced by the solver. Hence, to ensure that the returned value has full method accuracy one of the “tstop” modes may be used.
3.2.2. Interpolation
As mentioned above, the time-stepping modules in ARKODE support interpolation of solutions \(y(t_\text{out})\) and derivatives \(y^{(d)}(t_\text{out})\), where \(t_\text{out}\) occurs within a completed time step from \(t_{n-1} \to t_n\). Additionally, this module supports extrapolation of solutions and derivatives for \(t\) outside this interval (e.g. to construct predictors for iterative nonlinear and linear solvers). To this end, ARKODE currently supports construction of polynomial interpolants \(p_q(t)\) of polynomial degree up to \(q=5\), although users may select interpolants of lower degree.
ARKODE provides two complementary interpolation approaches, both of which are accessible from any of the time-stepping modules: “Hermite” and “Lagrange”. The former approach has been included with ARKODE since its inception, and is more suitable for non-stiff problems; the latter is a new approach that is designed to provide increased accuracy when integrating stiff problems. Both are described in detail below.
3.2.2.1. Hermite interpolation module
For non-stiff problems, polynomial interpolants of Hermite form are provided. Rewriting the IVP (3.5) in standard form,
we typically construct temporal interpolants using the data \(\left\{ y_{n-1}, \hat{f}_{n-1}, y_{n}, \hat{f}_{n} \right\}\), where here we use the simplified notation \(\hat{f}_{k}\) to denote \(\hat{f}(t_k,y_k)\). Defining a normalized “time” variable, \(\tau\), for the most-recently-computed solution interval \(t_{n-1} \to t_{n}\) as
we then construct the interpolants \(p_q(t)\) as follows:
\(q=0\): constant interpolant
\[p_0(\tau) = \frac{y_{n-1} + y_{n}}{2}.\]\(q=1\): linear Lagrange interpolant
\[p_1(\tau) = -\tau\, y_{n-1} + (1+\tau)\, y_{n}.\]\(q=2\): quadratic Hermite interpolant
\[p_2(\tau) = \tau^2\,y_{n-1} + (1-\tau^2)\,y_{n} + h_n(\tau+\tau^2)\,\hat{f}_{n}.\]\(q=3\): cubic Hermite interpolant
\[p_3(\tau) = (3\tau^2 + 2\tau^3)\,y_{n-1} + (1-3\tau^2-2\tau^3)\,y_{n} + h_n(\tau^2+\tau^3)\,\hat{f}_{n-1} + h_n(\tau+2\tau^2+\tau^3)\,\hat{f}_{n}.\]\(q=4\): quartic Hermite interpolant
\[\begin{split}p_4(\tau) &= (-6\tau^2 - 16\tau^3 - 9\tau^4)\,y_{n-1} + (1 + 6\tau^2 + 16\tau^3 + 9\tau^4)\,y_{n} + \frac{h_n}{4}(-5\tau^2 - 14\tau^3 - 9\tau^4)\,\hat{f}_{n-1} \\ &+ h_n(\tau + 2\tau^2 + \tau^3)\,\hat{f}_{n} + \frac{27 h_n}{4}(-\tau^4 - 2\tau^3 - \tau^2)\,\hat{f}_a,\end{split}\]where \(\hat{f}_a=\hat{f}\left(t_{n} - \dfrac{h_n}{3},p_3\left(-\dfrac13\right)\right)\). We point out that interpolation at this degree requires an additional evaluation of the full right-hand side function \(\hat{f}(t,y)\), thereby increasing its cost in comparison with \(p_3(t)\).
\(q=5\): quintic Hermite interpolant
\[\begin{split}p_5(\tau) &= (54\tau^5 + 135\tau^4 + 110\tau^3 + 30\tau^2)\,y_{n-1} + (1 - 54\tau^5 - 135\tau^4 - 110\tau^3 - 30\tau^2)\,y_{n} \\ &+ \frac{h_n}{4}(27\tau^5 + 63\tau^4 + 49\tau^3 + 13\tau^2)\,\hat{f}_{n-1} + \frac{h_n}{4}(27\tau^5 + 72\tau^4 + 67\tau^3 + 26\tau^2 + \tau)\,\hat{f}_n \\ &+ \frac{h_n}{4}(81\tau^5 + 189\tau^4 + 135\tau^3 + 27\tau^2)\,\hat{f}_a + \frac{h_n}{4}(81\tau^5 + 216\tau^4 + 189\tau^3 + 54\tau^2)\,\hat{f}_b,\end{split}\]where \(\hat{f}_a=\hat{f}\left(t_{n} - \dfrac{h_n}{3},p_4\left(-\dfrac13\right)\right)\) and \(\hat{f}_b=\hat{f}\left(t_{n} - \dfrac{2h_n}{3},p_4\left(-\dfrac23\right)\right)\). We point out that interpolation at this degree requires four additional evaluations of the full right-hand side function \(\hat{f}(t,y)\), thereby significantly increasing its cost over \(p_4(t)\).
We note that although interpolants of order \(q > 5\) are possible, these are not currently implemented due to their increased computing and storage costs.
3.2.2.2. Lagrange interpolation module
For stiff problems where \(\hat{f}\) may have large Lipschitz constant, polynomial interpolants of Lagrange form are provided. These interpolants are constructed using the data \(\left\{ y_{n}, y_{n-1}, \ldots, y_{n-\nu} \right\}\) where \(0\le\nu\le5\). These polynomials have the form
Since we assume that the solutions \(y_{n-j}\) have length much larger than \(\nu\le5\) in ARKODE-based simulations, we evaluate \(p\) at any desired \(t\in\mathbb{R}\) by first evaluating the Lagrange polynomial basis functions at the input value for \(t\), and then performing a simple linear combination of the vectors \(\{y_k\}_{k=0}^{\nu}\). Derivatives \(p^{(d)}(t)\) may be evaluated similarly as
however since the algorithmic complexity involved in evaluating derivatives of the Lagrange basis functions increases dramatically as the derivative order grows, our Lagrange interpolation module currently only provides derivatives up to \(d=3\).
We note that when using this interpolation module, during the first \((\nu-1)\) steps of integration we do not have sufficient solution history to construct the full \(\nu\)-degree interpolant. Therefore during these initial steps, we construct the highest-degree interpolants that are currently available at the moment, achieving the full \(\nu\)-degree interpolant once these initial steps have completed.
3.2.3. ARKStep – Additive Runge–Kutta methods
The ARKStep time-stepping module in ARKODE is designed for IVPs of the form
i.e. the right-hand side function is additively split into two components:
\(f^E(t,y)\) contains the “nonstiff” components of the system (this will be integrated using an explicit method);
\(f^I(t,y)\) contains the “stiff” components of the system (this will be integrated using an implicit method);
and the left-hand side may include a nonsingular, possibly time-dependent, matrix \(M(t)\).
In solving the IVP (3.6), we first consider the corresponding problem in standard form,
where \(\hat{f}^E(t,y) = M(t)^{-1}\,f^E(t,y)\) and \(\hat{f}^I(t,y) = M(t)^{-1}\,f^I(t,y)\). ARKStep then utilizes variable-step, embedded, additive Runge–Kutta methods (ARK), corresponding to algorithms of the form
Here \(\tilde{y}_n\) are embedded solutions that approximate \(y(t_n)\) and are used for error estimation; these typically have slightly lower accuracy than the computed solutions \(y_n\). The internal stage times are abbreviated using the notation \(t^E_{n,j} = t_{n-1} + c^E_j h_n\) and \(t^I_{n,j} = t_{n-1} + c^I_j h_n\). The ARK method is primarily defined through the coefficients \(A^E \in \mathbb{R}^{s\times s}\), \(A^I \in \mathbb{R}^{s\times s}\), \(b^E \in \mathbb{R}^{s}\), \(b^I \in \mathbb{R}^{s}\), \(c^E \in \mathbb{R}^{s}\) and \(c^I \in \mathbb{R}^{s}\), that correspond with the explicit and implicit Butcher tables. Additional coefficients \(\tilde{b}^E \in \mathbb{R}^{s}\) and \(\tilde{b}^I \in \mathbb{R}^{s}\) are used to construct the embedding \(\tilde{y}_n\). We note that ARKStep currently enforces the constraint that the explicit and implicit methods in an ARK pair must share the same number of stages, \(s\). We note that except when the problem has a time-independent mass matrix \(M\), ARKStep allows the possibility for different explicit and implicit abscissae, i.e. \(c^E\) need not equal \(c^I\).
The user of ARKStep must choose appropriately between one of three classes of methods: ImEx, explicit, and implicit. All of the built-in Butcher tables encoding the coefficients \(c^E\), \(c^I\), \(A^E\), \(A^I\), \(b^E\), \(b^I\), \(\tilde{b}^E\) and \(\tilde{b}^I\) are further described in the section §3.8.
For mixed stiff/nonstiff problems, a user should provide both of the functions \(f^E\) and \(f^I\) that define the IVP system. For such problems, ARKStep currently implements the ARK methods proposed in [56, 80, 83], allowing for methods having order of accuracy \(q = \{2,3,4,5\}\) and embeddings with orders \(p = \{1,2,3,4\}\); the tables for these methods are given in section §3.8.3. Additionally, user-defined ARK tables are supported.
For nonstiff problems, a user may specify that \(f^I = 0\), i.e. the equation (3.6) reduces to the non-split IVP
In this scenario, the coefficients \(A^I=0\), \(c^I=0\), \(b^I=0\) and \(\tilde{b}^I=0\) in (3.8), and the ARK methods reduce to classical explicit Runge–Kutta methods (ERK). For these classes of methods, ARKODE provides coefficients with orders of accuracy \(q = \{2,3,4,5,6,7,8,9\}\), with embeddings of orders \(p = \{1,2,3,4,5,6,7,8\}\). These default to the methods in sections §3.8.1.1, §3.8.1.3, §3.8.1.8, §3.8.1.12, §3.8.1.17, and §3.8.1.20, respectively. As with ARK methods, user-defined ERK tables are supported.
Alternately, for stiff problems the user may specify that \(f^E = 0\), so the equation (3.6) reduces to the non-split IVP
Similarly to ERK methods, in this scenario the coefficients \(A^E=0\), \(c^E=0\), \(b^E=0\) and \(\tilde{b}^E=0\) in (3.8), and the ARK methods reduce to classical diagonally-implicit Runge–Kutta methods (DIRK). For these classes of methods, ARKODE provides tables with orders of accuracy \(q = \{2,3,4,5\}\), with embeddings of orders \(p = \{1,2,3,4\}\). These default to the methods §3.8.2.1, §3.8.2.9, §3.8.2.12, and §3.8.2.21, respectively. Again, user-defined DIRK tables are supported.
3.2.4. ERKStep – Explicit Runge–Kutta methods
The ERKStep time-stepping module in ARKODE is designed for IVP of the form
i.e., unlike the more general problem form (3.6), ERKStep requires that problems have an identity mass matrix (i.e., \(M(t)=I\)) and that the right-hand side function is not split into separate components.
For such problems, ERKStep provides variable-step, embedded, explicit Runge–Kutta methods (ERK), corresponding to algorithms of the form
where the variables have the same meanings as in the previous section.
Clearly, the problem (3.11) is fully encapsulated in the more general problem (3.9), and the algorithm (3.12) is similarly encapsulated in the more general algorithm (3.8). While it therefore follows that ARKStep can be used to solve every problem solvable by ERKStep, using the same set of methods, we include ERKStep as a distinct time-stepping module since this simplified form admits a more efficient and memory-friendly implementation than the more general form (3.11).
3.2.5. SPRKStep – Symplectic Partitioned Runge–Kutta methods
The SPRKStep time-stepping module in ARKODE is designed for problems where the state vector is partitioned as
and the component partitioned IVP is given by
The right-hand side functions \(f_1(t,p)\) and \(f_2(t,q)\) typically arise from the separable Hamiltonian system
where
When H is autonomous, then H is a conserved quantity. Often this corresponds to the conservation of energy (for example, in n-body problems). For non-autonomous H, the invariants are no longer directly obtainable from the Hamiltonian [119].
In practice, the ordering of the variables does not matter and is determined by the user. SPRKStep utilizes Symplectic Partitioned Runge-Kutta (SPRK) methods represented by the pair of explicit and diagonally implicit Butcher tableaux,
These methods approximately conserve a nearby Hamiltonian for exponentially long times [62]. SPRKStep makes the assumption that the Hamiltonian is separable, in which case the resulting method is explicit. SPRKStep provides schemes with order of accuracy and conservation equal to \(q = \{1,2,3,4,5,6,8,10\}\). The references for these these methods and the default methods used are given in the section §3.8.4.
In the default case, the algorithm for a single time-step is as follows (for autonomous Hamiltonian systems the times provided to \(f_1\) and \(f_2\) can be ignored).
Set \(P_0 = p_{n-1}, Q_1 = q_{n-1}\)
For \(i = 1,\ldots,s\) do:
\(P_i = P_{i-1} + h_n \hat{a}_i f_1(t_{n-1} + \hat{c}_i h_n, Q_i)\)
\(Q_{i+1} = Q_i + h_n a_i f_2(t_{n-1} + c_i h_n, P_i)\)
Set \(p_n = P_s, q_n = Q_{s+1}\)
Optionally, a different algorithm leveraging compensated summation can be used that is more robust to roundoff error at the expense of 2 extra vector operations per stage and an additional 5 per time step. It also requires one extra vector to be stored. However, it is signficantly more robust to roundoff error accumulation [117]. When compensated summation is enabled, the following incremental form is used to compute a time step:
Set \(\Delta P_0 = 0, \Delta Q_1 = 0\)
For \(i = 1,\ldots,s\) do:
\(\Delta P_i = \Delta P_{i-1} + h_n \hat{a}_i f_1(t_{n-1} + \hat{c}_i h_n, q_{n-1} + \Delta Q_i)\)
\(\Delta Q_{i+1} = \Delta Q_i + h_n a_i f_2(t_{n-1} + c_i h_n, p_{n-1} + \Delta P_i)\)
Set \(\Delta p_n = \Delta P_s, \Delta q_n = \Delta Q_{s+1}\)
Using compensated summation, set \(p_n = p_{n-1} + \Delta p_n, q_n = q_{n-1} + \Delta q_n\)
Since temporal error based adaptive time-stepping is known to ruin the conservation property [62], SPRKStep employs a fixed time-step size.
3.2.6. MRIStep – Multirate infinitesimal step methods
The MRIStep time-stepping module in ARKODE is designed for IVPs of the form
i.e., the right-hand side function is additively split into three components:
\(f^E(t,y)\) contains the “slow-nonstiff” components of the system (this will be integrated using an explicit method and a large time step \(h^S\)),
\(f^I(t,y)\) contains the “slow-stiff” components of the system (this will be integrated using an implicit method and a large time step \(h^S\)), and
\(f^F(t,y)\) contains the “fast” components of the system (this will be integrated using a possibly different method than the slow time scale and a small time step \(h^F \ll h^S\)).
As with ERKStep, MRIStep currently requires that problems be posed with an identity mass matrix, \(M(t)=I\). The slow time scale may consist of only nonstiff terms (\(f^I \equiv 0\)), only stiff terms (\(f^E \equiv 0\)), or both nonstiff and stiff terms.
For cases with only a single slow right-hand side function (i.e., \(f^E \equiv 0\) or \(f^I \equiv 0\)), MRIStep provides fixed-slow-step multirate infinitesimal step (MIS) [105, 106, 107] and multirate infinitesimal GARK (MRI-GARK) [103] methods. For problems with an additively split slow right-hand side MRIStep provides fixed-slow-step implicit-explicit MRI-GARK (IMEX-MRI-GARK) [36] methods. The slow (outer) method derives from an \(s\) stage Runge–Kutta method for MIS and MRI-GARK methods or an additive Runge–Kutta method for IMEX-MRI-GARK methods. In either case, the stage values and the new solution are computed by solving an auxiliary ODE with a fast (inner) time integration method. This corresponds to the following algorithm for a single step:
Set \(z_1 = y_{n-1}\).
For \(i = 2,\ldots,s+1\) do:
Let \(t_{n,i-1}^S = t_{n-1} + c_{i-1}^S h^S\) and \(v(t_{n,i-1}^S) = z_{i-1}\).
Let \(r_i(t) = \frac{1}{\Delta c_i^S} \sum\limits_{j=1}^{i-1} \omega_{i,j}(\tau) f^E(t_{n,j}^I, z_j) + \frac{1}{\Delta c_i^S} \sum\limits_{j=1}^i \gamma_{i,j}(\tau) f^I(t_{n,j}^I, z_j)\) where \(\Delta c_i^S=\left(c^S_i - c^S_{i-1}\right)\) and the normalized time is \(\tau = (t - t_{n,i-1}^S)/(h^S \Delta c_i^S)\).
For \(t \in [t_{n,i-1}^S, t_{n,i}^S]\) solve \(\dot{v}(t) = f^F(t, v) + r_i(t)\).
Set \(z_i = v(t_{n,i}^S)\).
Set \(y_{n} = z_{s+1}\).
The fast (inner) IVP solve can be carried out using either the ARKStep module (allowing for explicit, implicit, or ImEx treatments of the fast time scale with fixed or adaptive steps), or a user-defined integration method (see section §3.4.5.4).
The final abscissa is \(c^S_{s+1}=1\) and the coefficients \(\omega_{i,j}\) and \(\gamma_{i,j}\) are polynomials in time that dictate the couplings from the slow to the fast time scale; these can be expressed as in [36] and [103] as
and where the tables \(\Omega^{\{k\}}\in\mathbb{R}^{(s+1)\times(s+1)}\) and \(\Gamma^{\{k\}}\in\mathbb{R}^{(s+1)\times(s+1)}\) define the slow-to-fast coupling for the explicit and implicit components respectively.
For traditional MIS methods, the coupling coefficients are uniquely defined based on a slow Butcher table \((A^S,b^S,c^S)\) having an explicit first stage (i.e., \(c^S_1=0\) and \(A^S_{1,j}=0\) for \(1\le j\le s\)), sorted abscissae (i.e., \(c^S_{i} \ge c^S_{i-1}\) for \(2\le i\le s\)), and the final abscissa is \(c^S_s \leq 1\). With these properties met, the coupling coefficients for an explicit-slow method are given as
For general slow tables \((A^S,b^S,c^S)\) with at least second-order accuracy, the corresponding MIS method will be second order. However, if this slow table is at least third order and satisfies the additional condition
where \(\mathbf{e}_j\) corresponds to the \(j\)-th column from the \(s \times s\) identity matrix, then the overall MIS method will be third order.
In the above algorithm, when the slow (outer) method has repeated abscissa, i.e. \(\Delta c_i^S = 0\) for stage \(i\), the fast (inner) IVP can be rescaled and integrated analytically. In this case the stage is computed as
which corresponds to a standard ARK, DIRK, or ERK stage computation depending on whether the summations over \(k\) are zero or nonzero.
As with standard ARK and DIRK methods, implicitness at the slow time scale is characterized by nonzero values on or above the diagonal of the matrices \(\Gamma^{\{k\}}\). Typically, MRI-GARK and IMEX-MRI-GARK methods are at most diagonally-implicit (i.e., \(\gamma_{i,j}^{\{k\}}=0\) for all \(j>i\)). Furthermore, diagonally-implicit stages are characterized as being “solve-decoupled” if \(\Delta c_i^S = 0\) when \(\gamma_{i,i}^{\{k\}} \ne 0\), in which case the stage is computed as standard ARK or DIRK update. Alternately, a diagonally-implicit stage \(i\) is considered “solve-coupled” if \(\Delta c^S_i \gamma_{i,j}^{\{k\}} \ne 0\), in which case the stage solution \(z_i\) is both an input to \(r(t)\) and the result of time-evolution of the fast IVP, necessitating an implicit solve that is coupled to the fast (inner) solver. At present, only “solve-decoupled” diagonally-implicit MRI-GARK and IMEX-MRI-GARK methods are supported.
For problems with only a slow-nonstiff term (\(f^I \equiv 0\)), MRIStep provides third and fourth order explicit MRI-GARK methods. In cases with only a slow-stiff term (\(f^E \equiv 0\)), MRIStep supplies second, third, and fourth order implicit solve-decoupled MRI-GARK methods. For applications with both stiff and nonstiff slow terms, MRIStep implements third and fourth order IMEX-MRI-GARK methods. For a complete list of the methods available in MRIStep see §3.4.5.3.2. Additionally, users may supply their own method by defining and attaching a coupling table, see §3.4.5.3 for more information.
3.2.7. Error norms
In the process of controlling errors at various levels (time integration, nonlinear solution, linear solution), the methods in ARKODE use a weighted root-mean-square norm, denoted \(\|\cdot\|_\text{WRMS}\), for all error-like quantities,
The utility of this norm arises in the specification of the weighting vector \(w\), that combines the units of the problem with user-supplied values that specify an “acceptable” level of error. To this end, we construct an error weight vector using the most-recent step solution and user-supplied relative and absolute tolerances, namely
Since \(1/w_i\) represents a tolerance in the \(i\)-th component of the solution vector \(y\), a vector whose WRMS norm is 1 is regarded as “small.” For brevity, unless specified otherwise we will drop the subscript WRMS on norms in the remainder of this section.
Additionally, for problems involving a non-identity mass matrix, \(M\ne I\), the units of equation (3.6) may differ from the units of the solution \(y\). In this case, we may additionally construct a residual weight vector,
where the user may specify a separate absolute residual tolerance value or array, \(ATOL'\). The choice of weighting vector used in any given norm is determined by the quantity being measured: values having “solution” units use (3.20), whereas values having “equation” units use (3.21). Obviously, for problems with \(M=I\), the solution and equation units are identical, in which case the solvers in ARKODE will use (3.20) when computing all error norms.
3.2.8. Time step adaptivity
A critical component of IVP “solvers” (rather than just time-steppers) is their adaptive control of local truncation error (LTE). At every step, we estimate the local error, and ensure that it satisfies tolerance conditions. If this local error test fails, then the step is recomputed with a reduced step size. To this end, the Runge–Kutta methods packaged within both the ARKStep and ERKStep modules admit an embedded solution \(\tilde{y}_n\), as shown in equations (3.8) and (3.12). Generally, these embedded solutions attain a slightly lower order of accuracy than the computed solution \(y_n\). Denoting the order of accuracy for \(y_n\) as \(q\) and for \(\tilde{y}_n\) as \(p\), most of these embedded methods satisfy \(p = q-1\). These values of \(q\) and \(p\) correspond to the global orders of accuracy for the method and embedding, hence each admit local truncation errors satisfying [60]
where \(C\) and \(D\) are constants independent of \(h_n\), and where we have assumed exact initial conditions for the step, i.e. \(y_{n-1} = y(t_{n-1})\). Combining these estimates, we have
We therefore use the norm of the difference between \(y_n\) and \(\tilde{y}_n\) as an estimate for the LTE at the step \(n\)
for ARK methods, and similarly for ERK methods. Here, \(\beta>0\) is an error bias to help account for the error constant \(D\); the default value of this constant is \(\beta = 1.5\), which may be modified by the user.
With this LTE estimate, the local error test is simply \(\|T_n\| < 1\) since this norm includes the user-specified tolerances. If this error test passes, the step is considered successful, and the estimate is subsequently used to determine the next step size, the algorithms used for this purpose are described in §3.2.8. If the error test fails, the step is rejected and a new step size \(h'\) is then computed using the same error controller as for successful steps. A new attempt at the step is made, and the error test is repeated. If the error test fails twice, then \(h'/h\) is limited above to 0.3, and limited below to 0.1 after an additional step failure. After seven error test failures, control is returned to the user with a failure message. We note that all of the constants listed above are only the default values; each may be modified by the user.
We define the step size ratio between a prospective step \(h'\) and a completed step \(h\) as \(\eta\), i.e. \(\eta = h' / h\). This value is subsequently bounded from above by \(\eta_\text{max}\) to ensure that step size adjustments are not overly aggressive. This upper bound changes according to the step and history,
A flowchart detailing how the time steps are modified at each iteration to ensure solver convergence and successful steps is given in the figure below. Here, all norms correspond to the WRMS norm, and the error adaptivity function arkAdapt is supplied by one of the error control algorithms discussed in the subsections below.
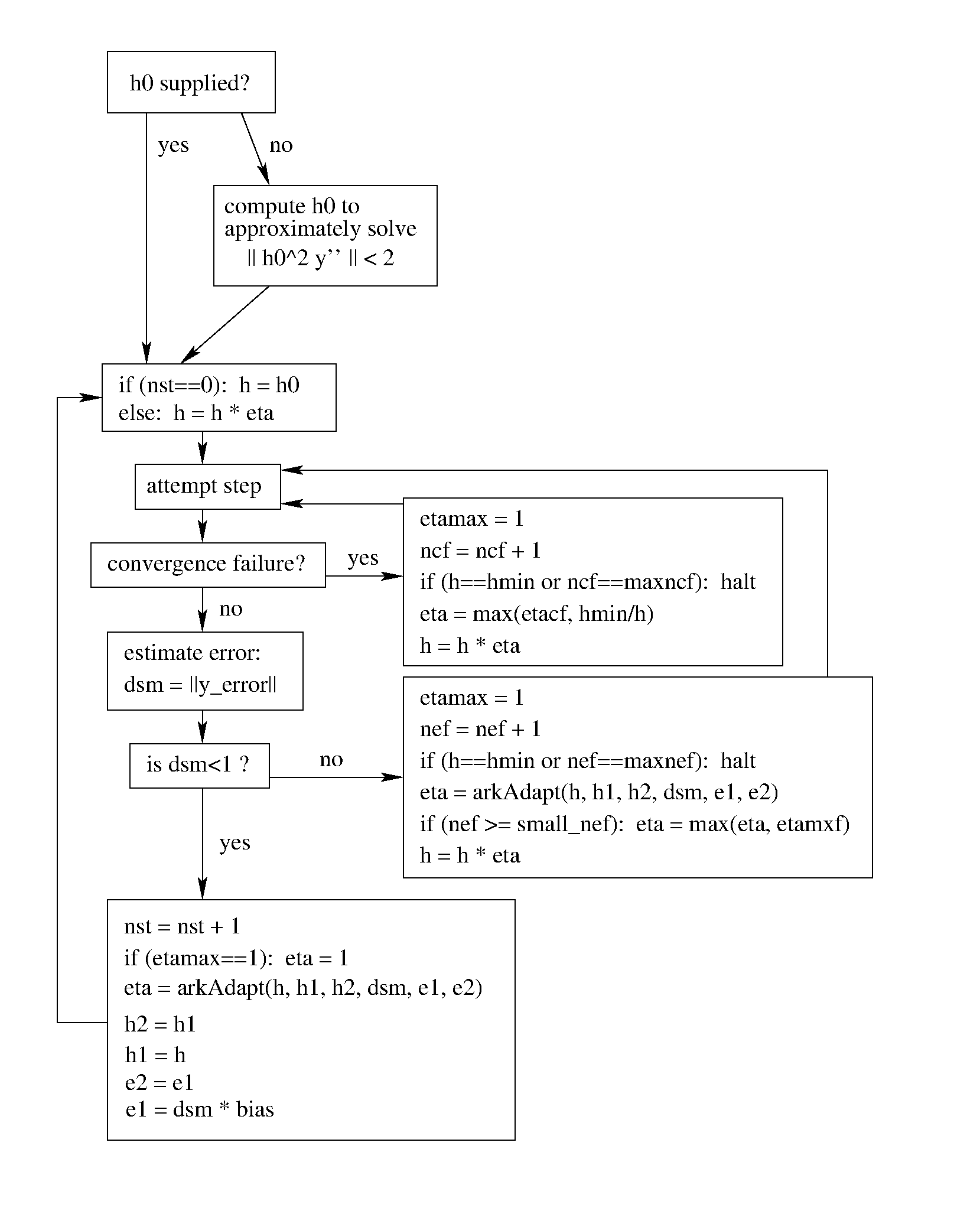
For some problems it may be preferable to avoid small step size adjustments. This can be especially true for problems that construct a Newton Jacobian matrix or a preconditioner for a nonlinear or an iterative linear solve, where this construction is computationally expensive, and where convergence can be seriously hindered through use of an inaccurate matrix. To accommodate these scenarios, the step is left unchanged when \(\eta \in [\eta_L, \eta_U]\). The default values for this interval are \(\eta_L = 1\) and \(\eta_U = 1.5\), and may be modified by the user.
We note that any choices for \(\eta\) (or equivalently, \(h'\)) are subsequently constrained by the optional user-supplied bounds \(h_\text{min}\) and \(h_\text{max}\). Additionally, the time-stepping algorithms in ARKODE may similarly limit \(h'\) to adhere to a user-provided “TSTOP” stopping point, \(t_\text{stop}\).
The time-stepping modules in ARKODE adapt the step size in order to attain local errors within desired tolerances of the true solution. These adaptivity algorithms estimate the prospective step size \(h'\) based on the asymptotic local error estimates (3.22). We define the values \(\varepsilon_n\), \(\varepsilon_{n-1}\) and \(\varepsilon_{n-2}\) as
corresponding to the local error estimates for three consecutive steps, \(t_{n-3} \to t_{n-2} \to t_{n-1} \to t_n\). These local error history values are all initialized to 1 upon program initialization, to accommodate the few initial time steps of a calculation where some of these error estimates have not yet been computed. With these estimates, ARKODE supports one of two approaches for temporal error control.
First, any valid implementation of the SUNAdaptController class §13.1 may be used by ARKODE’s adaptive time-stepping modules to provide a candidate error-based prospective step size \(h'\).
Second, ARKODE’s adaptive time-stepping modules currently still allow the user to define their own time step adaptivity function,
allowing for problem-specific choices, or for continued experimentation with temporal error controllers. We note that this support has been deprecated in favor of the SUNAdaptController class, and will be removed in a future release.
3.2.9. Explicit stability
For problems that involve a nonzero explicit component, i.e. \(f^E(t,y) \ne 0\) in ARKStep or for any problem in ERKStep, explicit and ImEx Runge–Kutta methods may benefit from additional user-supplied information regarding the explicit stability region. All ARKODE adaptivity methods utilize estimates of the local error, and it is often the case that such local error control will be sufficient for method stability, since unstable steps will typically exceed the error control tolerances. However, for problems in which \(f^E(t,y)\) includes even moderately stiff components, and especially for higher-order integration methods, it may occur that a significant number of attempted steps will exceed the error tolerances. While these steps will automatically be recomputed, such trial-and-error can result in an unreasonable number of failed steps, increasing the cost of the computation. In these scenarios, a stability-based time step controller may also be useful.
Since the maximum stable explicit step for any method depends on the problem under consideration, in that the value \((h_n\lambda)\) must reside within a bounded stability region, where \(\lambda\) are the eigenvalues of the linearized operator \(\partial f^E / \partial y\), information on the maximum stable step size is not readily available to ARKODE’s time-stepping modules. However, for many problems such information may be easily obtained through analysis of the problem itself, e.g. in an advection-diffusion calculation \(f^I\) may contain the stiff diffusive components and \(f^E\) may contain the comparably nonstiff advection terms. In this scenario, an explicitly stable step \(h_\text{exp}\) would be predicted as one satisfying the Courant-Friedrichs-Lewy (CFL) stability condition for the advective portion of the problem,
where \(\Delta x\) is the spatial mesh size and \(\lambda\) is the fastest advective wave speed.
In these scenarios, a user may supply a routine to predict this maximum explicitly stable step size, \(|h_\text{exp}|\). If a value for \(|h_\text{exp}|\) is supplied, it is compared against the value resulting from the local error controller, \(|h_\text{acc}|\), and the eventual time step used will be limited accordingly,
Here the explicit stability step factor \(c>0\) (often called the “CFL number”) defaults to \(1/2\) but may be modified by the user.
3.2.10. Fixed time stepping
While both the ARKStep and ERKStep time-stepping modules are designed for tolerance-based time step adaptivity, they additionally support a “fixed-step” mode. This mode is typically used for debugging purposes, for verification against hand-coded Runge–Kutta methods, or for problems where the time steps should be chosen based on other problem-specific information. In this mode, all internal time step adaptivity is disabled:
temporal error control is disabled,
nonlinear or linear solver non-convergence will result in an error (instead of a step size adjustment),
no check against an explicit stability condition is performed.
Note
Since temporal error based adaptive time-stepping is known to ruin the conservation property of SPRK methods, SPRKStep employs a fixed time-step size by default.
Note
Fixed-step mode is currently required for the slow time scale in the MRIStep module.
Additional information on this mode is provided in the sections ARKStep Optional Inputs, ERKStep Optional Inputs, SPRKStep Optional Inputs, and MRIStep Optional Inputs.
3.2.11. Algebraic solvers
When solving a problem involving either an implicit component (e.g., in ARKStep with \(f^I(t,y) \ne 0\), or in MRIStep with a solve-decoupled implicit slow stage), or a non-identity mass matrix (\(M(t) \ne I\) in ARKStep), systems of linear or nonlinear algebraic equations must be solved at each stage and/or step of the method. This section therefore focuses on the variety of mathematical methods provided in the ARKODE infrastructure for such problems, including nonlinear solvers, linear solvers, preconditioners, iterative solver error control, implicit predictors, and techniques used for simplifying the above solves when using different classes of mass-matrices.
3.2.11.1. Nonlinear solver methods
For the DIRK and ARK methods corresponding to (3.6) and (3.10) in ARKStep, and the solve-decoupled implicit slow stages (3.18) in MRIStep, an implicit system
must be solved for each implicit stage \(z_i\). In order to maximize solver efficiency, we define this root-finding problem differently based on the type of mass-matrix supplied by the user.
In the case that \(M=I\) within ARKStep, we define the residual as
(3.25)\[G(z_i) \equiv z_i - h_n A^I_{i,i} f^I(t^I_{n,i}, z_i) - a_i,\]where we have the data
\[a_i \equiv y_{n-1} + h_n \sum_{j=1}^{i-1} \left[ A^E_{i,j} f^E(t^E_{n,j}, z_j) + A^I_{i,j} f^I(t^I_{n,j}, z_j) \right].\]In the case of non-identity mass matrix \(M\ne I\) within ARKStep, but where \(M\) is independent of \(t\), we define the residual as
(3.26)\[G(z_i) \equiv M z_i - h_n A^I_{i,i} f^I(t^I_{n,i}, z_i) - a_i,\]where we have the data
\[a_i \equiv M y_{n-1} + h_n \sum_{j=1}^{i-1} \left[ A^E_{i,j} f^E(t^E_{n,j}, z_j) + A^I_{i,j} f^I(t^I_{n,j}, z_j) \right].\]Note
This form of residual, as opposed to \(G(z_i) = z_i - h_n A^I_{i,i} \hat{f}^I(t^I_{n,i}, z_i) - a_i\) (with \(a_i\) defined appropriately), removes the need to perform the nonlinear solve with right-hand side function \(\hat{f}^I=M^{-1}\,f^I\), as that would require a linear solve with \(M\) at every evaluation of the implicit right-hand side routine.
In the case of ARKStep with \(M\) dependent on \(t\), we define the residual as
(3.27)\[G(z_i) \equiv M(t^I_{n,i}) (z_i - a_i) - h_n A^I_{i,i} f^I(t^I_{n,i}, z_i)\]where we have the data
\[a_i \equiv y_{n-1} + h_n \sum_{j=1}^{i-1} \left[ A^E_{i,j} \hat{f}^E(t^E_{n,j}, z_j) + A^I_{i,j} \hat{f}^I(t^I_{n,j}, z_j) \right].\]Note
As above, this form of the residual is chosen to remove excessive mass-matrix solves from the nonlinear solve process.
Similarly, in MRIStep (that always assumes \(M=I\)), we have the residual
(3.28)\[G(z_i) \equiv z_i - h^S \left(\sum_{k\geq 0} \frac{\gamma_{i,i}^{\{k\}}}{k+1}\right) f^I(t_{n,i}^S, z_i) - a_i = 0\]where
\[a_i \equiv z_{i-1} + h^S \sum_{j=1}^{i-1} \left(\sum_{k\geq 0} \frac{\gamma_{i,j}^{\{k\}}}{k+1}\right)f^I(t_{n,j}^S, z_j).\]
Upon solving for \(z_i\), method stages must store \(f^E(t^E_{n,j}, z_i)\) and \(f^I(t^I_{n,j}, z_i)\). It is possible to compute the latter without evaluating \(f^I\) after each nonlinear solve. Consider, for example, (3.25) which implies
(3.29)\[f^I(t^I_{n,j}, z_i) = \frac{z_i - a_i}{h_n A^I_{i,i}}\]
when \(z_i\) is the exact root, and similar relations hold for non-identity
mass matrices. This optimization can be enabled by
ARKStepSetDeduceImplicitRhs() and MRIStepSetDeduceImplicitRhs()
with the second argument in either function set to SUNTRUE. Another factor to
consider when using this option is the amplification of errors from the
nonlinear solver to the stages. In (3.29), nonlinear
solver errors in \(z_i\) are scaled by \(1 / (h_n A^I_{i,i})\). By
evaluating \(f^I\) on \(z_i\), errors are scaled roughly by the Lipshitz
constant \(L\) of the problem. If \(h_n A^I_{i,i} L > 1\), which is
often the case when using implicit methods, it may be more accurate to use
(3.29). Additional details are discussed in
[110].
In each of the above nonlinear residual functions, if \(f^I(t,y)\) depends nonlinearly on \(y\) then (3.24) corresponds to a nonlinear system of equations; if instead \(f^I(t,y)\) depends linearly on \(y\) then this is a linear system of equations.
To solve each of the above root-finding problems ARKODE leverages SUNNonlinearSolver modules from the underlying SUNDIALS infrastructure (see section §12). By default, ARKODE selects a variant of Newton’s method,
where \(m\) is the Newton iteration index, and the Newton update \(\delta^{(m+1)}\) in turn requires the solution of the Newton linear system
in which
within ARKStep, or
within MRIStep.
In addition to Newton-based nonlinear solvers, the SUNDIALS SUNNonlinearSolver interface allows solvers of fixed-point type. These generally implement a fixed point iteration for solving an implicit stage \(z_i\),
Unlike with Newton-based nonlinear solvers, fixed-point iterations generally do not require the solution of a linear system involving the Jacobian of \(f\) at each iteration.
Finally, if the user specifies that \(f^I(t,y)\) depends linearly on \(y\) in ARKStep or MRIStep and if the Newton-based SUNNonlinearSolver module is used, then the problem (3.24) will be solved using only a single Newton iteration. In this case, an additional user-supplied argument indicates whether this Jacobian is time-dependent or not, signaling whether the Jacobian or preconditioner needs to be recomputed at each stage or time step, or if it can be reused throughout the full simulation.
The optimal choice of solver (Newton vs fixed-point) is highly problem dependent. Since fixed-point solvers do not require the solution of linear systems involving the Jacobian of \(f\), each iteration may be significantly less costly than their Newton counterparts. However, this can come at the cost of slower convergence (or even divergence) in comparison with Newton-like methods. While a Newton-based iteration is the default solver in ARKODE due to its increased robustness on very stiff problems, we strongly recommend that users also consider the fixed-point solver when attempting a new problem.
For either the Newton or fixed-point solvers, it is well-known that both the efficiency and robustness of the algorithm intimately depend on the choice of a good initial guess. The initial guess for these solvers is a prediction \(z_i^{(0)}\) that is computed explicitly from previously-computed data (e.g. \(y_{n-2}\), \(y_{n-1}\), and \(z_j\) where \(j<i\)). Additional information on the specific predictor algorithms is provided in section §3.2.11.5.
3.2.11.2. Linear solver methods
When a Newton-based method is chosen for solving each nonlinear system, a linear system of equations must be solved at each nonlinear iteration. For this solve ARKODE leverages another component of the shared SUNDIALS infrastructure, the “SUNLinearSolver,” described in section §11. These linear solver modules are grouped into two categories: matrix-based linear solvers and matrix-free iterative linear solvers. ARKODE’s interfaces for linear solves of these types are described in the subsections below.
3.2.11.2.1. Matrix-based linear solvers
In the case that a matrix-based linear solver is selected, a modified Newton iteration is utilized. In a modified Newton iteration, the matrix \({\mathcal A}\) is held fixed for multiple Newton iterations. More precisely, each Newton iteration is computed from the modified equation
in which
or
Here, the solution \(\tilde{z}\), time \(\tilde{t}\), and step size \(\tilde{h}\) upon which the modified equation rely, are merely values of these quantities from a previous iteration. In other words, the matrix \(\tilde{\mathcal A}\) is only computed rarely, and reused for repeated solves. As described below in section §3.2.11.2.3, the frequency at which \(\tilde{\mathcal A}\) is recomputed defaults to 20 time steps, but may be modified by the user.
When using the dense and band SUNMatrix objects for the linear systems (3.35), the Jacobian \(J\) may be supplied by a user routine, or approximated internally by finite-differences. In the case of differencing, we use the standard approximation
where \(e_j\) is the \(j\)-th unit vector, and the increments \(\sigma_j\) are given by
Here \(U\) is the unit roundoff, \(\sigma_0\) is a small dimensionless value, and \(w_j\) is the error weight defined in (3.20). In the dense case, this approach requires \(N\) evaluations of \(f^I\), one for each column of \(J\). In the band case, the columns of \(J\) are computed in groups, using the Curtis-Powell-Reid algorithm, with the number of \(f^I\) evaluations equal to the matrix bandwidth.
We note that with sparse and user-supplied SUNMatrix objects, the Jacobian must be supplied by a user routine.
3.2.11.2.2. Matrix-free iterative linear solvers
In the case that a matrix-free iterative linear solver is chosen, an inexact Newton iteration is utilized. Here, the matrix \({\mathcal A}\) is not itself constructed since the algorithms only require the product of this matrix with a given vector. Additionally, each Newton system (3.31) is not solved completely, since these linear solvers are iterative (hence the “inexact” in the name). As a result. for these linear solvers \({\mathcal A}\) is applied in a matrix-free manner,
The mass matrix-vector products \(Mv\) must be provided through a user-supplied routine; the Jacobian matrix-vector products \(Jv\) are obtained by either calling an optional user-supplied routine, or through a finite difference approximation to the directional derivative:
where we use the increment \(\sigma = 1/\|v\|\) to ensure that \(\|\sigma v\| = 1\).
As with the modified Newton method that reused \({\mathcal A}\) between solves, the inexact Newton iteration may also recompute the preconditioner \(P\) infrequently to balance the high costs of matrix construction and factorization against the reduced convergence rate that may result from a stale preconditioner.
3.2.11.2.3. Updating the linear solver
In cases where recomputation of the Newton matrix \(\tilde{\mathcal A}\) or preconditioner \(P\) is lagged, these structures will be recomputed only in the following circumstances:
when starting the problem,
when more than \(msbp = 20\) steps have been taken since the last update (this value may be modified by the user),
when the value \(\tilde{\gamma}\) of \(\gamma\) at the last update satisfies \(\left|\gamma/\tilde{\gamma} - 1\right| > \Delta\gamma_{max} = 0.2\) (this value may be modified by the user),
when a non-fatal convergence failure just occurred,
when an error test failure just occurred, or
if the problem is linearly implicit and \(\gamma\) has changed by a factor larger than 100 times machine epsilon.
When an update of \(\tilde{\mathcal A}\) or \(P\) occurs, it may or may not involve a reevaluation of \(J\) (in \(\tilde{\mathcal A}\)) or of Jacobian data (in \(P\)), depending on whether errors in the Jacobian were the likely cause for the update. Reevaluating \(J\) (or instructing the user to update \(P\)) occurs when:
starting the problem,
more than \(msbj=50\) steps have been taken since the last evaluation (this value may be modified by the user),
a convergence failure occurred with an outdated matrix, and the value \(\tilde{\gamma}\) of \(\gamma\) at the last update satisfies \(\left|\gamma/\tilde{\gamma} - 1\right| > 0.2\),
a convergence failure occurred that forced a step size reduction, or
if the problem is linearly implicit and \(\gamma\) has changed by a factor larger than 100 times machine epsilon.
However, for linear solvers and preconditioners that do not rely on costly matrix construction and factorization operations (e.g. when using a geometric multigrid method as preconditioner), it may be more efficient to update these structures more frequently than the above heuristics specify, since the increased rate of linear/nonlinear solver convergence may more than account for the additional cost of Jacobian/preconditioner construction. To this end, a user may specify that the system matrix \({\mathcal A}\) and/or preconditioner \(P\) should be recomputed more frequently.
As will be further discussed in section §3.2.11.4, in the case of most Krylov methods, preconditioning may be applied on the left, right, or on both sides of \({\mathcal A}\), with user-supplied routines for the preconditioner setup and solve operations.
3.2.11.3. Iteration Error Control
3.2.11.3.1. Nonlinear iteration error control
ARKODE provides a customized stopping test to the SUNNonlinearSolver module used for solving equation (3.24). This test is related to the temporal local error test, with the goal of keeping the nonlinear iteration errors from interfering with local error control. Denoting the final computed value of each stage solution as \(z_i^{(m)}\), and the true stage solution solving (3.24) as \(z_i\), we want to ensure that the iteration error \(z_i - z_i^{(m)}\) is “small” (recall that a norm less than 1 is already considered within an acceptable tolerance).
To this end, we first estimate the linear convergence rate \(R_i\) of the nonlinear iteration. We initialize \(R_i=1\), and reset it to this value whenever \(\tilde{\mathcal A}\) or \(P\) are updated. After computing a nonlinear correction \(\delta^{(m)} = z_i^{(m)} - z_i^{(m-1)}\), if \(m>0\) we update \(R_i\) as
where the default factor \(c_r=0.3\) is user-modifiable.
Let \(y_n^{(m)}\) denote the time-evolved solution constructed using our approximate nonlinear stage solutions, \(z_i^{(m)}\), and let \(y_n^{(\infty)}\) denote the time-evolved solution constructed using exact nonlinear stage solutions. We then use the estimate
Therefore our convergence (stopping) test for the nonlinear iteration for each stage is
where the factor \(\epsilon\) has default value 0.1. We default to a maximum of 3 nonlinear iterations. We also declare the nonlinear iteration to be divergent if any of the ratios
with \(m>0\), where \(r_{div}\) defaults to 2.3. If convergence fails in the nonlinear solver with \({\mathcal A}\) current (i.e., not lagged), we reduce the step size \(h_n\) by a factor of \(\eta_{cf}=0.25\). The integration will be halted after \(max_{ncf}=10\) convergence failures, or if a convergence failure occurs with \(h_n = h_\text{min}\). However, since the nonlinearity of (3.24) may vary significantly based on the problem under consideration, these default constants may all be modified by the user.
3.2.11.3.2. Linear iteration error control
When a Krylov method is used to solve the linear Newton systems (3.31), its errors must also be controlled. To this end, we approximate the linear iteration error in the solution vector \(\delta^{(m)}\) using the preconditioned residual vector, e.g. \(r = P{\mathcal A}\delta^{(m)} + PG\) for the case of left preconditioning (the role of the preconditioner is further elaborated in the next section). In an attempt to ensure that the linear iteration errors do not interfere with the nonlinear solution error and local time integration error controls, we require that the norm of the preconditioned linear residual satisfies
Here \(\epsilon\) is the same value as that is used above for the nonlinear error control. The factor of 10 is used to ensure that the linear solver error does not adversely affect the nonlinear solver convergence. Smaller values for the parameter \(\epsilon_L\) are typically useful for strongly nonlinear or very stiff ODE systems, while easier ODE systems may benefit from a value closer to 1. The default value is \(\epsilon_L = 0.05\), which may be modified by the user. We note that for linearly implicit problems the tolerance (3.41) is similarly used for the single Newton iteration.
3.2.11.4. Preconditioning
When using an inexact Newton method to solve the nonlinear system (3.24), an iterative method is used repeatedly to solve linear systems of the form \({\mathcal A}x = b\), where \(x\) is a correction vector and \(b\) is a residual vector. If this iterative method is one of the scaled preconditioned iterative linear solvers supplied with SUNDIALS, their efficiency may benefit tremendously from preconditioning. A system \({\mathcal A}x=b\) can be preconditioned using any one of:
These Krylov iterative methods are then applied to a system with the matrix \(P^{-1}{\mathcal A}\), \({\mathcal A}P^{-1}\), or \(P_L^{-1} {\mathcal A} P_R^{-1}\), instead of \({\mathcal A}\). In order to improve the convergence of the Krylov iteration, the preconditioner matrix \(P\), or the product \(P_L P_R\) in the third case, should in some sense approximate the system matrix \({\mathcal A}\). Simultaneously, in order to be cost-effective the matrix \(P\) (or matrices \(P_L\) and \(P_R\)) should be reasonably efficient to evaluate and solve. Finding an optimal point in this trade-off between rapid convergence and low cost can be quite challenging. Good choices are often problem-dependent (for example, see [22] for an extensive study of preconditioners for reaction-transport systems).
Most of the iterative linear solvers supplied with SUNDIALS allow for all three types of preconditioning (left, right or both), although for non-symmetric matrices \({\mathcal A}\) we know of few situations where preconditioning on both sides is superior to preconditioning on one side only (with the product \(P = P_L P_R\)). Moreover, for a given preconditioner matrix, the merits of left vs. right preconditioning are unclear in general, so we recommend that the user experiment with both choices. Performance can differ between these since the inverse of the left preconditioner is included in the linear system residual whose norm is being tested in the Krylov algorithm. As a rule, however, if the preconditioner is the product of two matrices, we recommend that preconditioning be done either on the left only or the right only, rather than using one factor on each side. An exception to this rule is the PCG solver, that itself assumes a symmetric matrix \({\mathcal A}\), since the PCG algorithm in fact applies the single preconditioner matrix \(P\) in both left/right fashion as \(P^{-1/2} {\mathcal A} P^{-1/2}\).
Typical preconditioners are based on approximations to the system Jacobian, \(J = \partial f^I / \partial y\). Since the Newton iteration matrix involved is \({\mathcal A} = M - \gamma J\), any approximation \(\bar{J}\) to \(J\) yields a matrix that is of potential use as a preconditioner, namely \(P = M - \gamma \bar{J}\). Because the Krylov iteration occurs within a Newton iteration and further also within a time integration, and since each of these iterations has its own test for convergence, the preconditioner may use a very crude approximation, as long as it captures the dominant numerical features of the system. We have found that the combination of a preconditioner with the Newton-Krylov iteration, using even a relatively poor approximation to the Jacobian, can be surprisingly superior to using the same matrix without Krylov acceleration (i.e., a modified Newton iteration), as well as to using the Newton-Krylov method with no preconditioning.
3.2.11.5. Implicit predictors
For problems with implicit components, a prediction algorithm is employed for constructing the initial guesses for each implicit Runge–Kutta stage, \(z_i^{(0)}\). As is well-known with nonlinear solvers, the selection of a good initial guess can have dramatic effects on both the speed and robustness of the solve, making the difference between rapid quadratic convergence versus divergence of the iteration. To this end, a variety of prediction algorithms are provided. In each case, the stage guesses \(z_i^{(0)}\) are constructed explicitly using readily-available information, including the previous step solutions \(y_{n-1}\) and \(y_{n-2}\), as well as any previous stage solutions \(z_j, \quad j<i\). In most cases, prediction is performed by constructing an interpolating polynomial through existing data, which is then evaluated at the desired stage time to provide an inexpensive but (hopefully) reasonable prediction of the stage solution. Specifically, for most Runge–Kutta methods each stage solution satisfies
(similarly for MRI methods \(z_i \approx y(t^S_{n,i})\)), so by constructing an interpolating polynomial \(p_q(t)\) through a set of existing data, the initial guess at stage solutions may be approximated as
As the stage times for MRI stages and implicit ARK and DIRK stages usually have non-negative abscissae (i.e., \(c_j^I > 0\)), it is typically the case that \(t^I_{n,j}\) (resp., \(t^S_{n,j}\)) is outside of the time interval containing the data used to construct \(p_q(t)\), hence (3.42) will correspond to an extrapolant instead of an interpolant. The dangers of using a polynomial interpolant to extrapolate values outside the interpolation interval are well-known, with higher-order polynomials and predictions further outside the interval resulting in the greatest potential inaccuracies.
The prediction algorithms available in ARKODE therefore construct a variety of interpolants \(p_q(t)\), having different polynomial order and using different interpolation data, to support “optimal” choices for different types of problems, as described below. We note that due to the structural similarities between implicit ARK and DIRK stages in ARKStep, and solve-decoupled implicit stages in MRIStep, we use the ARKStep notation throughout the remainder of this section, but each statement equally applies to MRIStep (unless otherwise noted).
3.2.11.5.1. Trivial predictor
The so-called “trivial predictor” is given by the formula
While this piecewise-constant interpolant is clearly not a highly accurate candidate for problems with time-varying solutions, it is often the most robust approach for highly stiff problems, or for problems with implicit constraints whose violation may cause illegal solution values (e.g. a negative density or temperature).
3.2.11.5.2. Maximum order predictor
At the opposite end of the spectrum, ARKODE’s interpolation modules discussed in section §3.2.2 can be used to construct a higher-order polynomial interpolant, \(p_q(t)\). The implicit stage predictor is computed through evaluating the highest-degree-available interpolant at each stage time \(t^I_{n,i}\).
3.2.11.5.3. Variable order predictor
This predictor attempts to use higher-degree polynomials \(p_q(t)\) for predicting earlier stages, and lower-degree interpolants for later stages. It uses the same interpolation module as described above, but chooses the polynomial degree adaptively based on the stage index \(i\), under the assumption that the stage times are increasing, i.e. \(c^I_j < c^I_k\) for \(j<k\):
3.2.11.5.4. Cutoff order predictor
This predictor follows a similar idea as the previous algorithm, but monitors the actual stage times to determine the polynomial interpolant to use for prediction. Denoting \(\tau = c_i^I \dfrac{h_n}{h_{n-1}}\), the polynomial degree \(q_i\) is chosen as:
3.2.11.5.5. Bootstrap predictor (\(M=I\) only) – deprecated
This predictor does not use any information from the preceding step, instead using information only within the current step \([t_{n-1},t_n]\). In addition to using the solution and ODE right-hand side function, \(y_{n-1}\) and \(f(t_{n-1},y_{n-1})\), this approach uses the right-hand side from a previously computed stage solution in the same step, \(f(t_{n-1}+c^I_j h,z_j)\) to construct a quadratic Hermite interpolant for the prediction. If we define the constants \(\tilde{h} = c^I_j h\) and \(\tau = c^I_i h\), the predictor is given by
For stages without a nonzero preceding stage time, i.e. \(c^I_j\ne 0\) for \(j<i\), this method reduces to using the trivial predictor \(z_i^{(0)} = y_{n-1}\). For stages having multiple preceding nonzero \(c^I_j\), we choose the stage having largest \(c^I_j\) value, to minimize the level of extrapolation used in the prediction.
We note that in general, each stage solution \(z_j\) has significantly worse accuracy than the time step solutions \(y_{n-1}\), due to the difference between the stage order and the method order in Runge–Kutta methods. As a result, the accuracy of this predictor will generally be rather limited, but it is provided for problems in which this increased stage error is better than the effects of extrapolation far outside of the previous time step interval \([t_{n-2},t_{n-1}]\).
Although this approach could be used with non-identity mass matrix, support for that mode is not currently implemented, so selection of this predictor in the case of a non-identity mass matrix will result in use of the trivial predictor.
Note
This predictor has been deprecated, and will be removed from a future release.
3.2.11.5.6. Minimum correction predictor (ARKStep, \(M=I\) only) – deprecated
The final predictor is not interpolation based; instead it utilizes all existing stage information from the current step to create a predictor containing all but the current stage solution. Specifically, as discussed in equations (3.8) and (3.24), each stage solves a nonlinear equation
This prediction method merely computes the predictor \(z_i\) as
Again, although this approach could be used with non-identity mass matrix, support for that mode is not currently implemented, so selection of this predictor in the case of a non-identity mass matrix will result in use of the trivial predictor.
Note
This predictor has been deprecated, and will be removed from a future release.
3.2.11.6. Mass matrix solver (ARKStep only)
Within the ARKStep algorithms described above, there are multiple locations where a matrix-vector product
or a linear solve
is required.
Of course, for problems in which \(M=I\) both of these operators are trivial. However for problems with non-identity mass matrix, these linear solves (3.44) may be handled using any valid SUNLinearSolver module, in the same manner as described in the section §3.2.11.2 for solving the linear Newton systems.
For ERK methods involving non-identity mass matrix, even though calculation of individual stages does not require an algebraic solve, both of the above operations (matrix-vector product, and mass matrix solve) may be required within each time step. Therefore, for these users we recommend reading the rest of this section as it pertains to ARK methods, with the obvious simplification that since \(f^E=f\) and \(f^I=0\) no Newton or fixed-point nonlinear solve, and no overall system linear solve, is involved in the solution process.
At present, for DIRK and ARK problems using a matrix-based solver for
the Newton nonlinear iterations, the type of matrix (dense, band,
sparse, or custom) for the Jacobian matrix \(J\) must match the
type of mass matrix \(M\), since these are combined to form the
Newton system matrix \(\tilde{\mathcal A}\). When matrix-based
methods are employed, the user must supply a routine to compute
\(M(t)\) in the appropriate form to match the structure of
\({\mathcal A}\), with a user-supplied routine of type
ARKLsMassFn(). This matrix structure is used internally to
perform any requisite mass matrix-vector products (3.43).
When matrix-free methods are selected, a routine must be supplied to perform the mass-matrix-vector product, \(Mv\). As with iterative solvers for the Newton systems, preconditioning may be applied to aid in solution of the mass matrix systems (3.44). When using an iterative mass matrix linear solver, we require that the norm of the preconditioned linear residual satisfies
where again, \(\epsilon\) is the nonlinear solver tolerance parameter from (3.39). When using iterative system and mass matrix linear solvers, \(\epsilon_L\) may be specified separately for both tolerances (3.41) and (3.45).
In the algorithmic descriptions above there are five locations where a linear solve of the form (3.44) is required: (a) at each iteration of a fixed-point nonlinear solve, (b) in computing the Runge–Kutta right-hand side vectors \(\hat{f}^E_i\) and \(\hat{f}^I_i\), (c) in constructing the time-evolved solution \(y_n\), (d) in estimating the local temporal truncation error, and (e) in constructing predictors for the implicit solver iteration (see section §3.2.11.5.2). We note that different nonlinear solver approaches (i.e., Newton vs fixed-point) and different types of mass matrices (i.e., time-dependent versus fixed) result in different subsets of the above operations. We discuss each of these in the bullets below.
When using a fixed-point nonlinear solver, at each fixed-point iteration we must solve
\[M(t^I_{n,i})\, z_i^{(m+1)} = G\left(z_i^{(m)}\right), \quad m=0,1,\ldots\]for the new fixed-point iterate, \(z_i^{(m+1)}\).
In the case of a time-dependent mass matrix, to construct the Runge–Kutta right-hand side vectors we must solve
\[M(t^E_{n,i}) \hat{f}^{E}_i \ = \ f^{E}(t^E_{n,i},z_i) \quad\text{and}\quad M(t^I_{n,i}) \hat{f}^{I}_j \ = \ f^{I}(t^I_{n,i},z_i)\]for the vectors \(\hat{f}^{E}_i\) and \(\hat{f}^{I}_i\).
For fixed mass matrices, we construct the time-evolved solution \(y_n\) from equation (3.8) by solving
\[\begin{split}&M y_n \ = \ M y_{n-1} + h_n \sum_{i=1}^{s} \left( b^E_i f^E(t^E_{n,i}, z_i) + b^I_i f^I(t^I_{n,i}, z_i)\right), \\ \Leftrightarrow \qquad & \\ &M (y_n -y_{n-1}) \ = \ h_n \sum_{i=1}^{s} \left(b^E_i f^E(t^E_{n,i}, z_i) + b^I_i f^I(t^I_{n,i}, z_i)\right), \\ \Leftrightarrow \qquad & \\ &M \nu \ = \ h_n \sum_{i=1}^{s} \left(b^E_i f^E(t^E_{n,i}, z_i) + b^I_i f^I(t^I_{n,i}, z_i)\right),\end{split}\]for the update \(\nu = y_n - y_{n-1}\).
Similarly, we compute the local temporal error estimate \(T_n\) from equation (3.23) by solving systems of the form
(3.46)\[M\, T_n = h \sum_{i=1}^{s} \left[ \left(b^E_i - \tilde{b}^E_i\right) f^E(t^E_{n,i}, z_i) + \left(b^I_i - \tilde{b}^I_i\right) f^I(t^I_{n,i}, z_i) \right].\]For problems with either form of non-identity mass matrix, in constructing dense output and implicit predictors of degree 2 or higher (see the section §3.2.11.5.2 above), we compute the derivative information \(\hat{f}_k\) from the equation
\[M(t_n) \hat{f}_n = f^E(t_n, y_n) + f^I(t_n, y_n).\]
In total, for problems with fixed mass matrix, we require only two mass-matrix linear solves (3.44) per attempted time step, with one more upon completion of a time step that meets the solution accuracy requirements. When fixed time-stepping is used (\(h_n=h\)), the solve (3.46) is not performed at each attempted step.
Similarly, for problems with time-dependent mass matrix, we require \(2s\) mass-matrix linear solves (3.44) per attempted step, where \(s\) is the number of stages in the ARK method (only half of these are required for purely explicit or purely implicit problems, (3.9) or (3.10)), with one more upon completion of a time step that meets the solution accuracy requirements.
In addition to the above totals, when using a fixed-point nonlinear solver (assumed to require \(m\) iterations), we will need an additional \(ms\) mass-matrix linear solves (3.44) per attempted time step (but zero linear solves with the system Jacobian).
3.2.12. Rootfinding
All of the time-stepping modules in ARKODE also support a rootfinding feature. This means that, while integrating the IVP (3.5), these can also find the roots of a set of user-defined functions \(g_i(t,y)\) that depend on \(t\) and the solution vector \(y = y(t)\). The number of these root functions is arbitrary, and if more than one \(g_i\) is found to have a root in any given interval, the various root locations are found and reported in the order that they occur on the \(t\) axis, in the direction of integration.
Generally, this rootfinding feature finds only roots of odd multiplicity, corresponding to changes in sign of \(g_i(t, y(t))\), denoted \(g_i(t)\) for short. If a user root function has a root of even multiplicity (no sign change), it will almost certainly be missed due to the realities of floating-point arithmetic. If such a root is desired, the user should reformulate the root function so that it changes sign at the desired root.
The basic scheme used is to check for sign changes of any \(g_i(t)\) over each time step taken, and then (when a sign change is found) to home in on the root (or roots) with a modified secant method [65]. In addition, each time \(g\) is evaluated, ARKODE checks to see if \(g_i(t) = 0\) exactly, and if so it reports this as a root. However, if an exact zero of any \(g_i\) is found at a point \(t\), ARKODE computes \(g(t+\delta)\) for a small increment \(\delta\), slightly further in the direction of integration, and if any \(g_i(t+\delta) = 0\) also, ARKODE stops and reports an error. This way, each time ARKODE takes a time step, it is guaranteed that the values of all \(g_i\) are nonzero at some past value of \(t\), beyond which a search for roots is to be done.
At any given time in the course of the time-stepping, after suitable checking and adjusting has been done, ARKODE has an interval \((t_\text{lo}, t_\text{hi}]\) in which roots of the \(g_i(t)\) are to be sought, such that \(t_\text{hi}\) is further ahead in the direction of integration, and all \(g_i(t_\text{lo}) \ne 0\). The endpoint \(t_\text{hi}\) is either \(t_n\), the end of the time step last taken, or the next requested output time \(t_\text{out}\) if this comes sooner. The endpoint \(t_\text{lo}\) is either \(t_{n-1}\), or the last output time \(t_\text{out}\) (if this occurred within the last step), or the last root location (if a root was just located within this step), possibly adjusted slightly toward \(t_n\) if an exact zero was found. The algorithm checks \(g(t_\text{hi})\) for zeros, and it checks for sign changes in \((t_\text{lo}, t_\text{hi})\). If no sign changes are found, then either a root is reported (if some \(g_i(t_\text{hi}) = 0\)) or we proceed to the next time interval (starting at \(t_\text{hi}\)). If one or more sign changes were found, then a loop is entered to locate the root to within a rather tight tolerance, given by
Whenever sign changes are seen in two or more root functions, the one deemed most likely to have its root occur first is the one with the largest value of \(\left|g_i(t_\text{hi})\right| / \left| g_i(t_\text{hi}) - g_i(t_\text{lo})\right|\), corresponding to the closest to \(t_\text{lo}\) of the secant method values. At each pass through the loop, a new value \(t_\text{mid}\) is set, strictly within the search interval, and the values of \(g_i(t_\text{mid})\) are checked. Then either \(t_\text{lo}\) or \(t_\text{hi}\) is reset to \(t_\text{mid}\) according to which subinterval is found to have the sign change. If there is none in \((t_\text{lo}, t_\text{mid})\) but some \(g_i(t_\text{mid}) = 0\), then that root is reported. The loop continues until \(\left|t_\text{hi} - t_\text{lo} \right| < \tau\), and then the reported root location is \(t_\text{hi}\). In the loop to locate the root of \(g_i(t)\), the formula for \(t_\text{mid}\) is
where \(\alpha\) is a weight parameter. On the first two passes through the loop, \(\alpha\) is set to 1, making \(t_\text{mid}\) the secant method value. Thereafter, \(\alpha\) is reset according to the side of the subinterval (low vs high, i.e. toward \(t_\text{lo}\) vs toward \(t_\text{hi}\)) in which the sign change was found in the previous two passes. If the two sides were opposite, \(\alpha\) is set to 1. If the two sides were the same, \(\alpha\) is halved (if on the low side) or doubled (if on the high side). The value of \(t_\text{mid}\) is closer to \(t_\text{lo}\) when \(\alpha < 1\) and closer to \(t_\text{hi}\) when \(\alpha > 1\). If the above value of \(t_\text{mid}\) is within \(\tau /2\) of \(t_\text{lo}\) or \(t_\text{hi}\), it is adjusted inward, such that its fractional distance from the endpoint (relative to the interval size) is between 0.1 and 0.5 (with 0.5 being the midpoint), and the actual distance from the endpoint is at least \(\tau/2\).
Finally, we note that when running in parallel, ARKODE’s rootfinding module assumes that the entire set of root defining functions \(g_i(t,y)\) is replicated on every MPI rank. Since in these cases the vector \(y\) is distributed across ranks, it is the user’s responsibility to perform any necessary communication to ensure that \(g_i(t,y)\) is identical on each rank.
3.2.13. Inequality Constraints
The ARKStep and ERKStep modules in ARKODE permit the user to impose optional inequality constraints on individual components of the solution vector \(y\). Any of the following four constraints can be imposed: \(y_i > 0\), \(y_i < 0\), \(y_i \geq 0\), or \(y_i \leq 0\). The constraint satisfaction is tested after a successful step and before the error test. If any constraint fails, the step size is reduced and a flag is set to update the Jacobian or preconditioner if applicable. Rather than cutting the step size by some arbitrary factor, ARKODE estimates a new step size \(h'\) using a linear approximation of the components in \(y\) that failed the constraint test (including a safety factor of 0.9 to cover the strict inequality case). If a step fails to satisfy the constraints 10 times (a value which may be modified by the user) within a step attempt, or fails with the minimum step size, then the integration is halted and an error is returned. In this case the user may need to employ other strategies as discussed in §3.4.2.2.2 and §3.4.3.2.2 to satisfy the inequality constraints.
3.2.14. Relaxation Methods
When the solution of (3.5) is conservative or dissipative with respect to a smooth convex function \(\xi(y(t))\), it is desirable to have the numerical method preserve these properties. That is \(\xi(y_n) = \xi(y_{n-1}) = \ldots = \xi(y_{0})\) for conservative systems and \(\xi(y_n) \leq \xi(y_{n-1})\) for dissipative systems. For examples of such problems, see the references below and the citations there in.
For such problems, ARKODE supports relaxation methods [78, 84, 97, 98] applied to ERK, DIRK, or ARK methods to ensure dissipation or preservation of the global function. The relaxed solution is given by
where \(d\) is the update to \(y_n\) (i.e., \(h_n \sum_{i=1}^{s}(b^E_i \hat{f}^E_i + b^I_i \hat{f}^I_i)\) for ARKStep and \(h_n \sum_{i=1}^{s} b_i f_i\) for ERKStep) and \(r\) is the relaxation factor selected to ensure conservation or dissipation. Given an ERK, DIRK, or ARK method of at least second order with non-negative solution weights (i.e., \(b_i \geq 0\) for ERKStep or \(b^E_i \geq 0\) and \(b^I_i \geq 0\) for ARKStep), the factor \(r\) is computed by solving the auxiliary scalar nonlinear system
at the end of each time step. The estimated change in \(\xi\) is given by \(e \equiv h_n \sum_{i=1}^{s} \langle \xi'(z_i), b^E_i f^E_i + b^I_i f^I_i \rangle\) where \(\xi'\) is the Jacobian of \(\xi\).
Two iterative methods are provided for solving (3.48), Newton’s method and Brent’s method. When using Newton’s method (the default), the iteration is halted either when the residual tolerance is met, \(F(r^{(k)}) < \epsilon_{\mathrm{relax\_res}}\), or when the difference between successive iterates satisfies the relative and absolute tolerances, \(|\delta_r^{(k)}| = |r^{(k)} - r^{(k-1)}| < \epsilon_{\mathrm{relax\_rtol}} |r^{(k-1)}| + \epsilon_{\mathrm{relax\_atol}}\). Brent’s method applies the same residual tolerance check and additionally halts when the bisection update satisfies the relative and absolute tolerances, \(|0.5 (r_c - r^{k})| < \epsilon_{\mathrm{relax\_rtol}} |r^{(k)}| + 0.5 \epsilon_{\mathrm{relax\_atol}}\) where \(r_c\) and \(r^{(k)}\) bound the root.
If the nonlinear solve fails to meet the specified tolerances within the maximum allowed number of iterations, the step size is reduced by the factor \(\eta_\mathrm{rf}\) (default 0.25) and the step is repeated. Additionally, the solution of (3.48) should be \(r = 1 + \mathcal{O}(h_n^{q - 1})\) for a method of order \(q\) [98]. As such, limits are imposed on the range of relaxation values allowed (i.e., limiting the maximum change in step size due to relaxation). A relaxation value greater than \(r_\text{max}\) (default 1.2) or less than \(r_\text{min}\) (default 0.8), is considered as a failed relaxation application and the step will is repeated with the step size reduced by \(\eta_\text{rf}\).
For more information on utilizing relaxation Runge–Kutta methods, see §3.4.3.3 and §3.4.2.3.