3.3. Code Organization
3.3.1. ARKODE organization
The ARKODE package is written in the ANSI C language. The following summarizes the basic structure of the package, although knowledge of this structure is not necessary for its use.
The overall organization of the ARKODE package is shown in
Fig. 3.3. The central integration modules,
implemented in the files arkode.h, arkode_impl.h, arkode_butcher.h,
arkode.c, arkode_arkstep.c , arkode_erkstep.c, arkode_mristep.h,
and arkode_butcher.c, deal with the evaluation of integration stages, the
nonlinear solvers, estimation of the local truncation error, selection of step
size, and interpolation to user output points, among other issues. ARKODE
supports SUNNonlinearSolver modules in either root-finding or fixed-point form
(see section §12) for any nonlinearly implicit problems that
arise in computing each internal stage. When using Newton-based nonlinear
solvers, or when using a non-identity mass matrix \(M\ne I\), ARKODE has
flexibility in the choice of method used to solve the linear sub-systems that
arise. Therefore, for any user problem invoking the Newton solvers, or any user
problem with \(M\ne I\), one (or more) of the linear system solver modules
should be specified by the user; this/these are then invoked as needed during
the integration process.
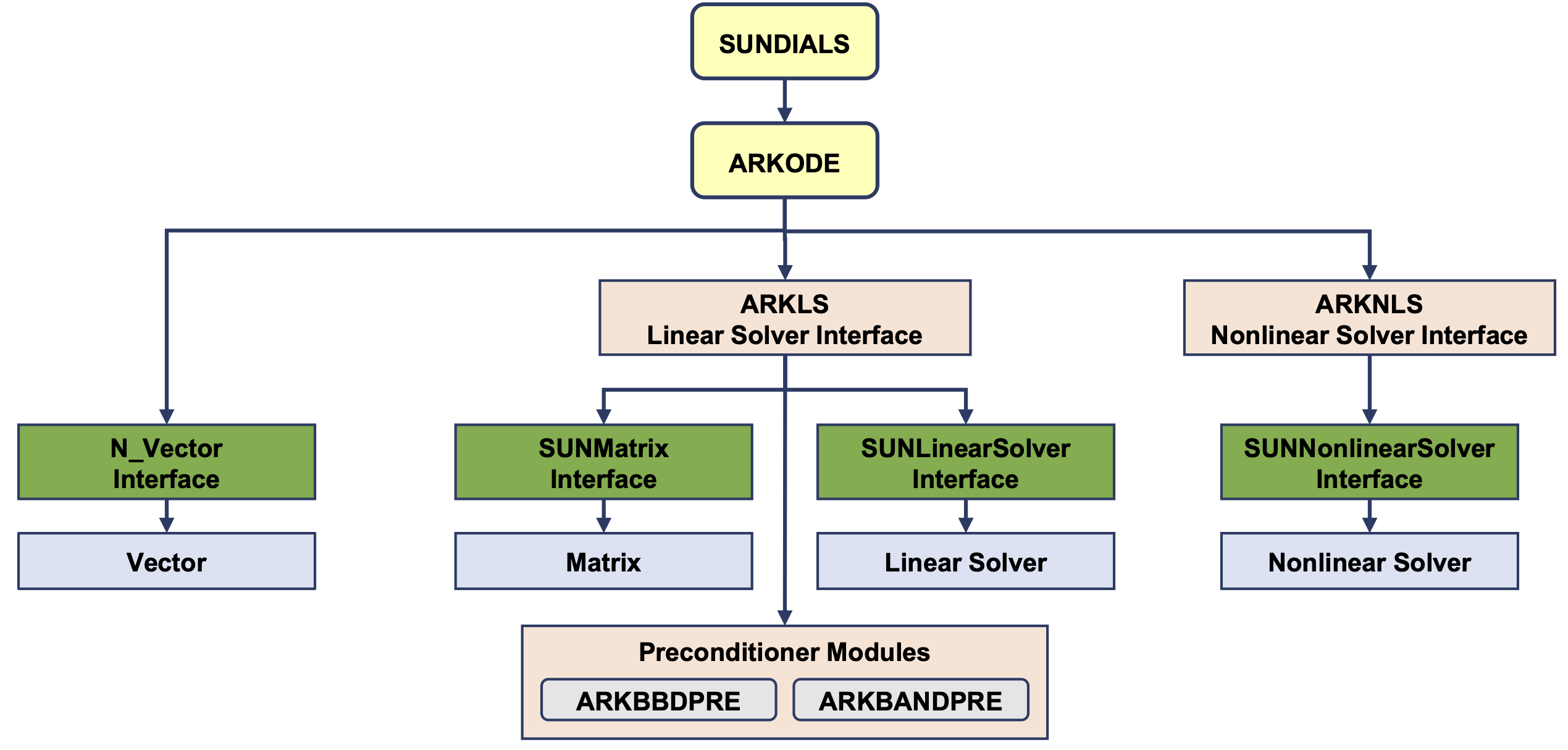
Fig. 3.3 ARKODE organization: Overall structure of the ARKODE package. Modules specific to ARKODE are the timesteppers (ARKODE), linear solver interfaces (ARKLS), nonlinear solver interfaces (ARKNLS), and preconditioners (ARKBANDPRE and ARKBBDPRE); all other items correspond to generic SUNDIALS vector, matrix, and solver modules.
For solving these linear systems, ARKODE’s linear solver interface supports both direct and iterative linear solvers adhering to the generic SUNLINSOL API (see §11). These solvers may utilize a SUNMATRIX object for storing Jacobian information, or they may be matrix-free. Since ARKODE can operate on any valid SUNLINSOL implementation, the set of linear solver modules available to ARKODE will expand as new SUNLINSOL modules are developed.
For preconditioned iterative methods with either the system or mass matrix solves, the preconditioning must be supplied by the user in two phases: setup and solve. While there is no default choice of preconditioner for generic problems, the references [22] and [27], together with the example and demonstration programs included with ARKODE and CVODE, offer considerable assistance in building simple preconditioners.
ARKODE also provides two rudimentary preconditioner modules, for use with any of the Krylov iterative linear solvers. The first, ARKBANDPRE is intended to be used with the serial or threaded vector data structures (NVECTOR_SERIAL, NVECTOR_OPENMP and NVECTOR_PTHREADS), and provides a banded difference-quotient approximation to the Jacobian as the preconditioner, with corresponding setup and solve routines. The second preconditioner module, ARKBBDPRE, is intended to work with the parallel vector data structure, NVECTOR_PARALLEL, and generates a preconditioner that is a block-diagonal matrix with each block being a band matrix owned by a single processor.
All state information used by ARKODE to solve a given problem is saved in a single opaque memory structure, and a pointer to that structure is returned to the user. For C, C++ and Fortran 2003 applications there is no global data in the ARKODE package, and so in this respect it is reentrant. State information specific to the linear solver interface is saved in a separate data structure, a pointer to which resides in the ARKODE memory structure. State information specific to the linear solver implementation (and matrix implementation, if applicable) are stored in their own data structures, that are returned to the user upon construction, and subsequently provided to ARKODE for use.