5.3. Code Organization

5.3.1. CVODES organization

The CVODES package is written in ANSI C. The following summarizes the basic structure of the package, although knowledge of this structure is not necessary for its use.

The overall organization of the CVODES package is shown in Fig. 5.4. The basic elements of the structure are a module for the basic integration algorithm (including forward sensitivity analysis), a module for adjoint sensitivity analysis, and support for the solution of nonlinear and linear systems that arise in the case of a stiff system.

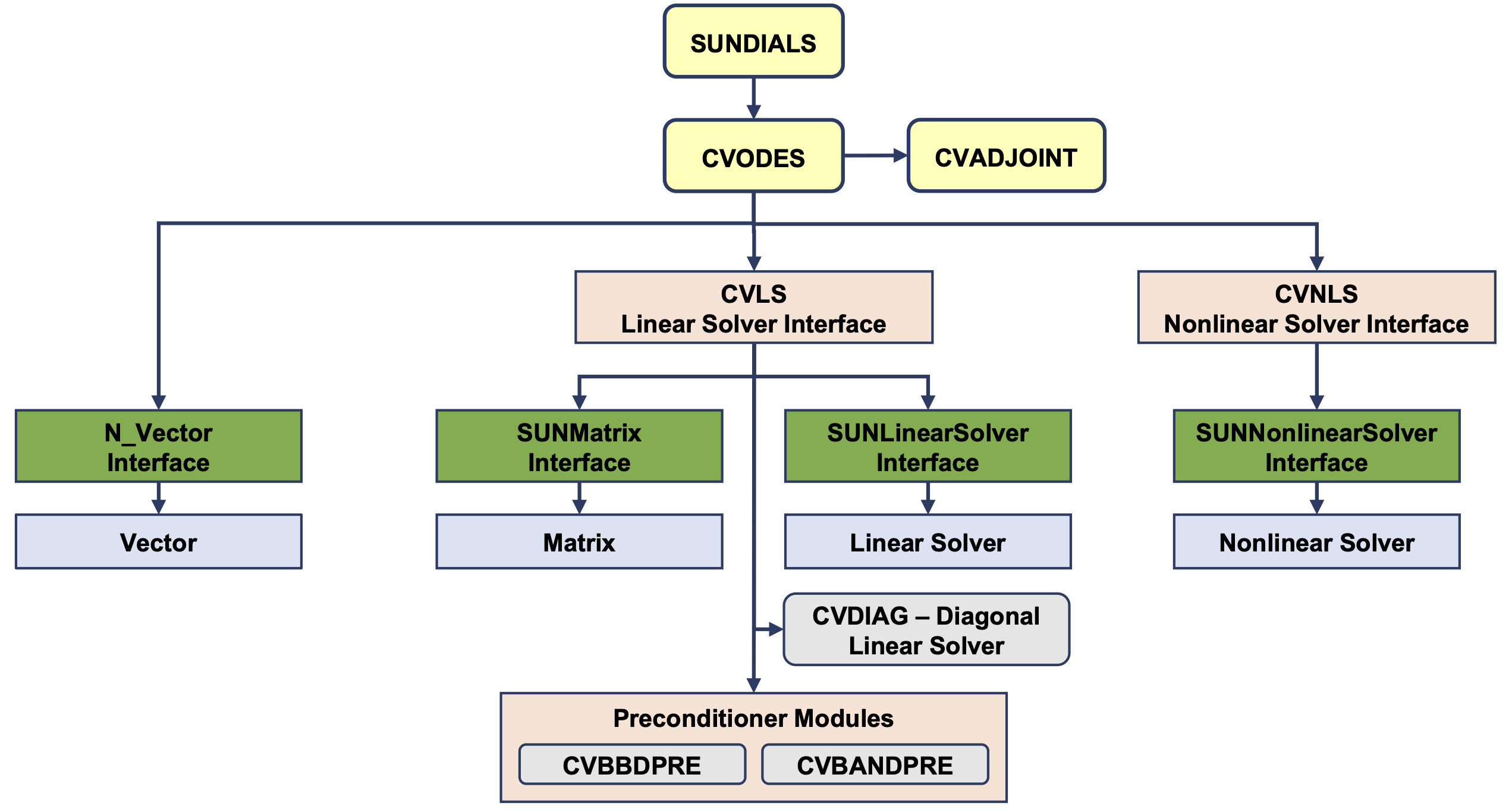
Fig. 5.4 Overall structure diagram of the CVODES package. Modules specific to CVODES begin with “CV” (CVLS, CVNLS, CVDIAG, CVBBDPRE, and CVBANDPRE), all other items correspond to generic SUNDIALS vector, matrix, and solver modules.

The central integration module, implemented in the files CVODES.h, cvode_impl.h, and CVODES.c, deals with the evaluation of integration coefficients, estimation of local error, selection of stepsize and order, and interpolation to user output points, among other issues.

CVODES utilizes generic linear and nonlinear solver modules defined by the SUNLinearSolver API (see Chapter §11) and SUNNonlinearSolver API (see Chapter §12), respectively. As such, CVODES has no knowledge of the method being used to solve the linear and nonlinear systems that arise. For any given user problem, there exists a single nonlinear solver interface and, if necessary, one of the linear system solver interfaces is specified, and invoked as needed during the integration.

In addition, if forward sensitivity analysis is turned on, the main module will integrate the forward sensitivity equations simultaneously with the original IVP. The sensitivity variables may be included in the local error control mechanism of the main integrator. CVODES provides three different strategies for dealing with the correction stage for the sensitivity variables: CV_SIMULTANEOUS, CV_STAGGERED and CV_STAGGERED1 (see §5.2.7 and §5.4.3.2.1). The CVODES package includes an algorithm for the approximation of the sensitivity equations right-hand sides by difference quotients, but the user has the option of supplying these right-hand sides directly.

The adjoint sensitivity module (file cvodea.c) provides the infrastructure needed for the backward integration of any system of ODEs which depends on the solution of the original IVP, in particular the adjoint system and any quadratures required in evaluating the gradient of the objective functional. This module deals with the setup of the checkpoints, the interpolation of the forward solution during the backward integration, and the backward integration of the adjoint equations.

At present, the package includes two linear solver interfaces. The primary linear solver interface, CVLS, supports both direct and iterative linear solvers built using the generic SUNLinearSolver API (see Chapter §11). These solvers may utilize a SUNMatrix object (see Chapter §10) for storing Jacobian information, or they may be matrix-free. Since CVODES can operate on any valid SUNLinearSolver implementation, the set of linear solver modules available to CVODES will expand as new SUNLinearSolver modules are developed.

Additionally, CVODES includes the diagonal linear solver interface, CVDIAG, that creates an internally generated diagonal approximation to the Jacobian.

For users employing SUNMATRIX_DENSE or SUNMATRIX_BAND Jacobian matrices, CVODES includes algorithms for their approximation through difference quotients, although the user also has the option of supplying a routine to compute the Jacobian (or an approximation to it) directly. This user-supplied routine is required when using sparse or user-supplied Jacobian matrices.

For users employing matrix-free iterative linear solvers, CVODES includes an algorithm for the approximation by difference quotients of the product \(Mv\). Again, the user has the option of providing routines for this operation, in two phases: setup (preprocessing of Jacobian data) and multiplication.

For preconditioned iterative methods, the preconditioning must be supplied by the user, again in two phases: setup and solve. While there is no default choice of preconditioner analogous to the difference-quotient approximation in the direct case, the references [22, 27], together with the example and demonstration programs included with CVODES, offer considerable assistance in building preconditioners.

CVODES’ linear solver interface consists of four primary phases, devoted to (1) memory allocation and initialization, (2) setup of the matrix data involved, (3) solution of the system, and (4) freeing of memory. The setup and solution phases are separate because the evaluation of Jacobians and preconditioners is done only periodically during the integration, and only as required to achieve convergence.

CVODES also provides two preconditioner modules, for use with any of the Krylov iterative linear solvers. The first one, CVBANDPRE, is intended to be used with NVECTOR_SERIAL, NVECTOR_OPENMP or NVECTOR_PTHREADS and provides a banded difference-quotient Jacobian-based preconditioner, with corresponding setup and solve routines. The second preconditioner module, CVBBDPRE, works in conjunction with NVECTOR_PARALLEL and generates a preconditioner that is a block-diagonal matrix with each block being a banded matrix.

All state information used by CVODES to solve a given problem is saved in a structure, and a pointer to that structure is returned to the user. There is no global data in the CVODES package, and so, in this respect, it is reentrant. State information specific to the linear solver is saved in a separate structure, a pointer to which resides in the CVODES memory structure. The reentrancy of CVODES was motivated by the anticipated multicomputer extension, but is also essential in a uniprocessor setting where two or more problems are solved by intermixed calls to the package from within a single user program.